Trigonometric Substitions

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\bigmath }[1]{$\displaystyle #1$} \newcommand {\choicebreak }[0]{} \newcommand {\type }[0]{} \newcommand {\notes }[0]{} \newcommand {\keywords }[0]{} \newcommand {\offline }[0]{} \newcommand {\comments }[0]{\begin {feedback}} \newcommand {\multiplechoice }[0]{\begin {multipleChoice}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

We practice executing trigonometric substitutions.

(Video) Calculus: Single Variable

Online Texts

Examples

(c.f. APEX Calculus Example 6.4.2) Compute the indefinite integral $\int \frac {dx}{\sqrt {5 + x^2}}.$

The structure of this integrand is adapted to a trigonometric substitution of type, so we let $x = \sqrt {5} \answer {\tan \theta }$ (type out the word theta). This gives $dx = \sqrt {5} \answer {\sec ^2 \theta }~d \theta$ .
We use the identity $\sec ^2 \theta = \tan ^2 \theta + 1$ , the quantity $5 + x^2$ can be rewritten using our substitution to equal $\answer {5 \sec ^2 \theta }$ . Therefore $\int \frac {dx}{\sqrt {5+x^2}} dx = \int \answer {\sec \theta } \, d \theta = \answer {\ln | \sec \theta + \tan \theta |} + C.$ (When writing out the indefinite integral, don’t forget absolute values.)
We construct a reference triangle compatible with our substitution. In this case, that means we need a right triangle with an angle $\theta$ which satisfies $x/\sqrt {5} = \tan \theta$ :
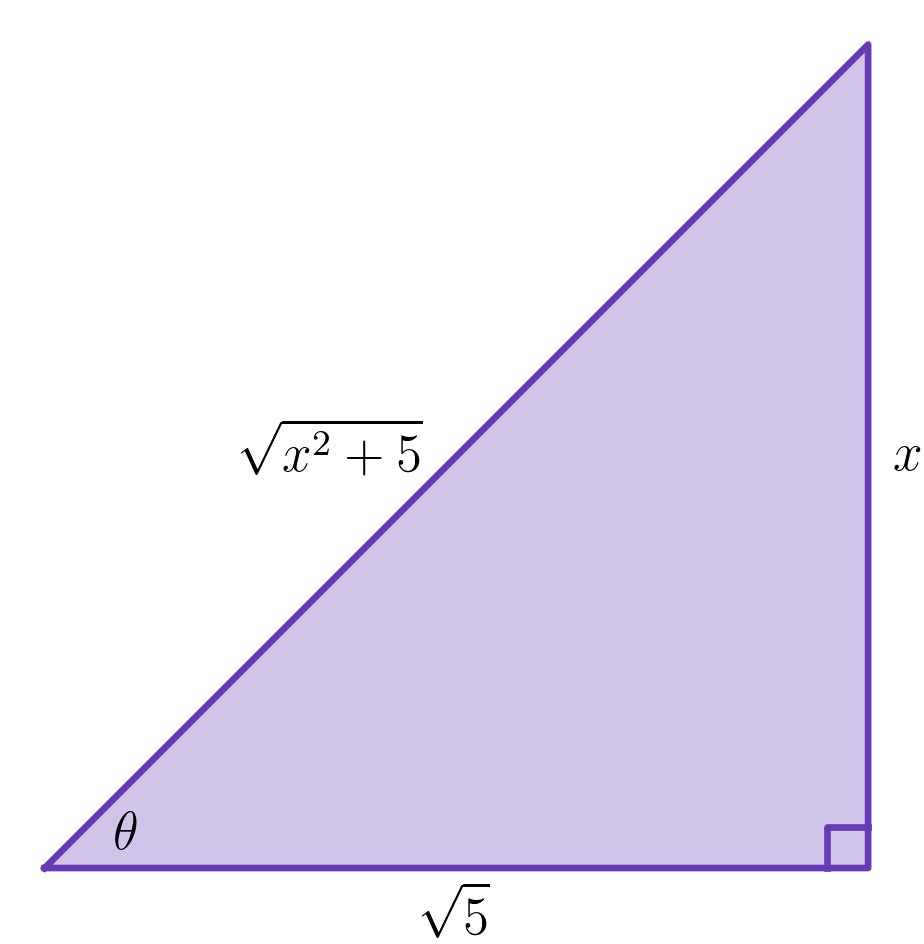
Using this reference triangle, we get that $\tan \theta = \frac {x}{\sqrt {5}} \qquad \sec \theta = \answer { \frac {\sqrt {x^2+5}}{\sqrt {5}}}.$ Using these formulas, we can write $\ln |\sec \theta + \tan \theta | = \ln \left | \answer {\frac {x}{\sqrt {5}} + \frac {\sqrt {x^2+5}}{\sqrt {5}}} \right | .$
We conclude that $\int \frac {dx}{\sqrt {x^2+5}} = \ln | x + \sqrt {x^2 + 5} | + C.$ (Note that the factor of $\sqrt {5}$ in the denominator of the logarithm is not necessary when we already have an arbitrary constant $C$ in our answer.)

Compute the indefinite integral $\int \frac {dx}{x^2 \sqrt {x^2 - 3}}.$

The structure of this integrand is adapted to a trigonometric substitution of type, so we let $x = \sqrt {3} \answer {\tan \theta }$ . This gives $dx = \sqrt {3} \answer {\sec \theta \tan \theta }~d \theta$ .
We use the identity $\sec ^2 \theta = \tan ^2 \theta + 1$ , the quantity $x^2 - 3$ can be rewritten using our substitution to equal $\answer {3 \tan ^2 \theta }$ . Therefore $\int \frac {dx}{x^2 \sqrt {x^2 - 3}} = \int \answer { \frac {\sqrt {3} \sec \theta \tan \theta }{3 \sec ^2 \theta \sqrt {3} \tan \theta }} d \theta = \answer {\frac {\sin \theta }{3}} + C.$
We construct a reference triangle compatible with our substitution. In this case, that means we need a right triangle with an angle $\theta$ which satisfies $x/\sqrt {3} = \sec \theta$ :
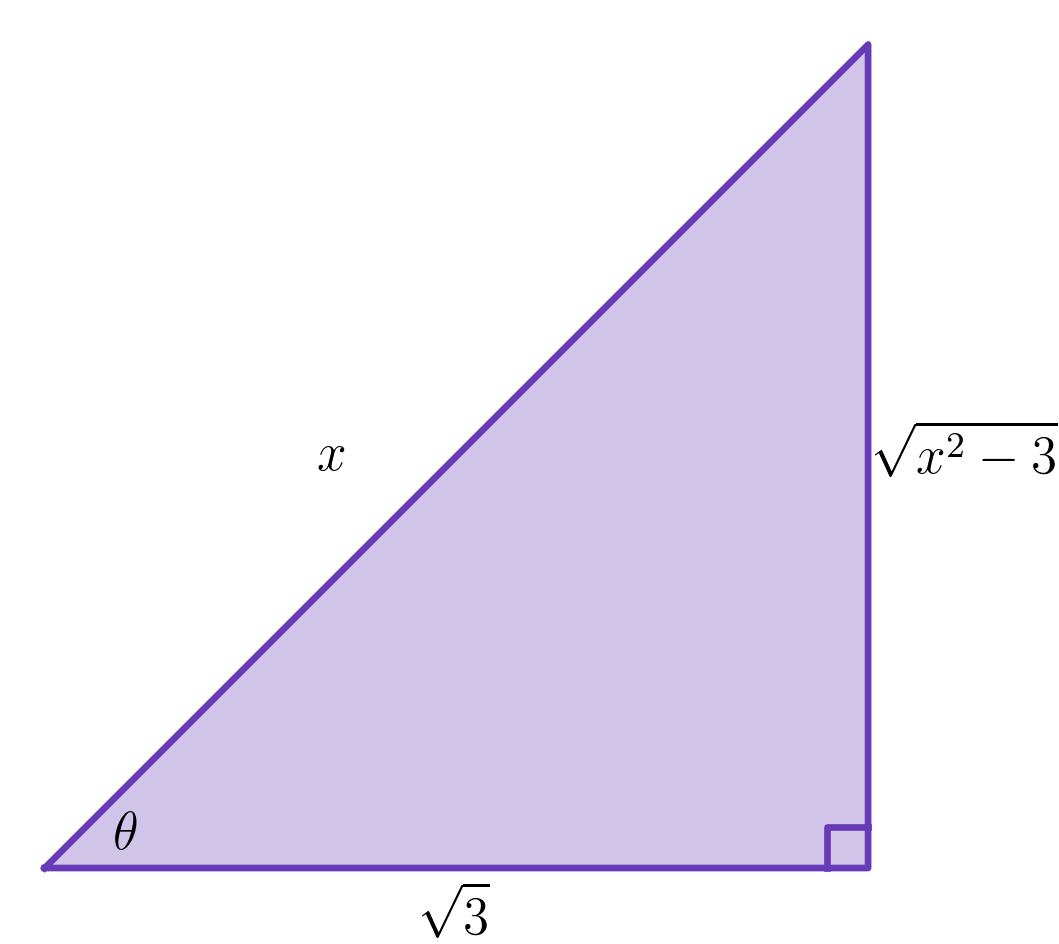
Using this reference triangle, we get that $\sin \theta = \answer {\frac {\sqrt {x^2-3}}{x}}.$
We conclude that $\int \frac {dx}{x^2 \sqrt {x^2-3}} = \answer { \frac {\sqrt {x^2-3}}{3x}} + C.$

(c.f. APEX Calculus Example 6.4.1) Compute the indefinite integral $\int \sqrt {9 - x^2} dx.$

The structure of this integrand is adapted to a trigonometric substitution of type, so we let $x = 3 \answer {\sin \theta }$ . This gives $dx = 3 \answer {\cos \theta }~d \theta$ .
Using the identity $\cos ^2 \theta + \sin ^2 \theta = 1$ , the expression $9 - x^2$ can be rewritten using the formula above as $\answer {(3 \cos \theta )^2}$ . Therefore $\int \sqrt {9-x^2} dx = \int \answer {9 (\cos \theta )^2} d \theta .$
We use the power reduction formula $\cos ^2 t = (1 + \cos 2t)/2$ and conclude $\int \sqrt {9-x^2} dx = \frac {9}{2} \int \left ( 1 + \cos 2 \theta \right ) d \theta = \frac {9}{2} \left [ \theta + \frac {1}{2} \sin 2 \theta \right ] + C.$
Now we construct a reference triangle which is compatible with the substitution we made. In this case, this means we need a right triangle for which $x/3 = \sin \theta$ :
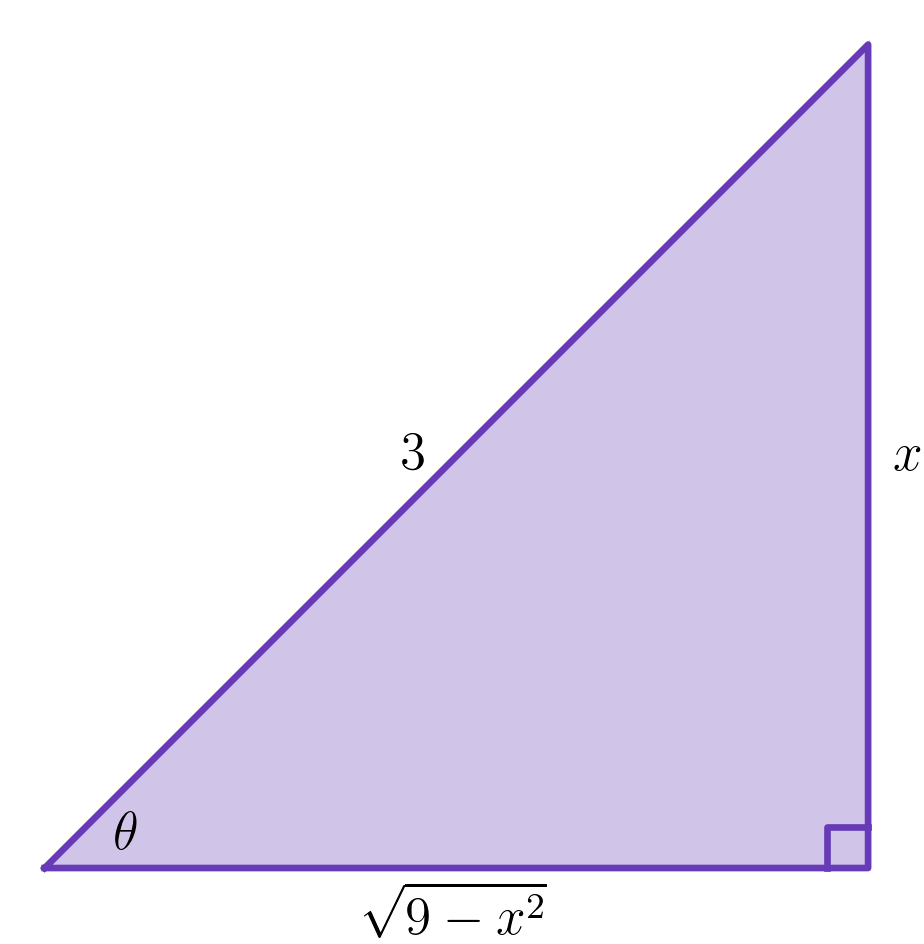
Using the reference triangle above, we have the identities $\sin \theta = \frac {x}{3} \qquad \cos \theta = \answer { \frac {\sqrt {9-x^2}}{3}} \qquad \theta = \arcsin \frac {x}{3}.$
The quantity $\sin 2 \theta$ is difficult to write as a function of $x$ as it stands, so we first use the double-angle formula $\sin 2 \theta = \cos \theta \sin \theta$ . We therefore conclude that $\int \sqrt {9-x^2} dx = \answer { \frac {9}{2} \left ( \arcsin \frac {x}{3} + \frac {x \sqrt {9-x^2}}{9} \right )} + C.$ (Note: Ximera will interpret $\sin ^{-1} x$ as $1/(\sin x)$ , so write $\arcsin$ when you mean inverse sine.)