Below you will find a slope field for the ODE $y' = -xy$.

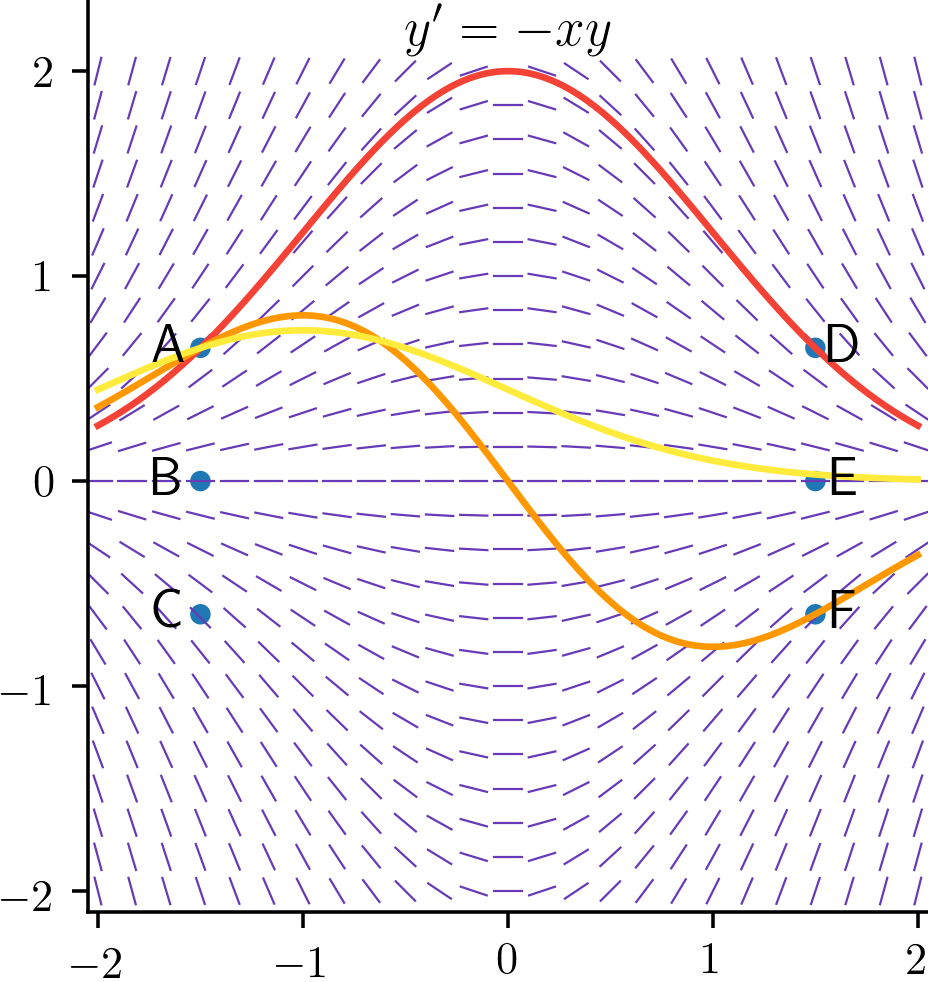
There are three curves shown: $$\begin {aligned} \text {In Red: } \ & {\displaystyle y = 2 e^{-\frac {x^2}{2}}}, \\ \text {In Orange: } \ & {\displaystyle y = -\frac {4x}{3} e^{-\frac {x^2}{2}}}, \\ \text {In Yellow: } \ & {\displaystyle y = e^{-\frac {x^2}{2} - x - \frac {3}{2}}}. \end {aligned}$$ Which of the three curves is a solution of the ODE $y' = -xy$? In other words, which of the three curves is correctly aligned with the slope field?

There are also a number of points marked on the graph: point B at $(-1.5,0)$, point C at $(-1.5,-0.65)$, point D at $(1.5,0.65)$, point E at $(1.5,0)$, and point F at $(1.5,-0.65)$. The solution of the ODE which begins at the point B will pass through the point DEF . Similarly, the solution which begins at C will pass through DEF .

Can two different solutions of the same first-order ODE $y' = f(x,y)$ have graphs which cross?

The concept behind Euler’s method is that we approximate a solution of an ODE of the form $y' = f(x,y)$ with a polygonal graph. Usually each segment of the graph has the same width (referred to as the step size). We use the function $f(x,y)$ to dictate the slope of each piece of the approximation. Let $y(x)$ be the solution to the initial value problem $y' = x + \frac {\ln y}{\ln 2} - \frac {y}{2}$ with $y(0) = 1$. Use Euler’s Method with step size $h = 1$ to approximate the value of $y(3)$.

• For this particular ODE, we have $$f(x,y) = \answer { x + \frac {\ln y}{\ln 2} - \frac {y}{2}}.$$
• Supposing that we start at the point$x = 0$, $y = 1$, the slope will be $$f(0,1) = \answer {-\frac {1}{2}.}$$
• Consider a line segment beginning at the point $(0,1)$ having slope $f(0,1)$ which you just calculated.

  

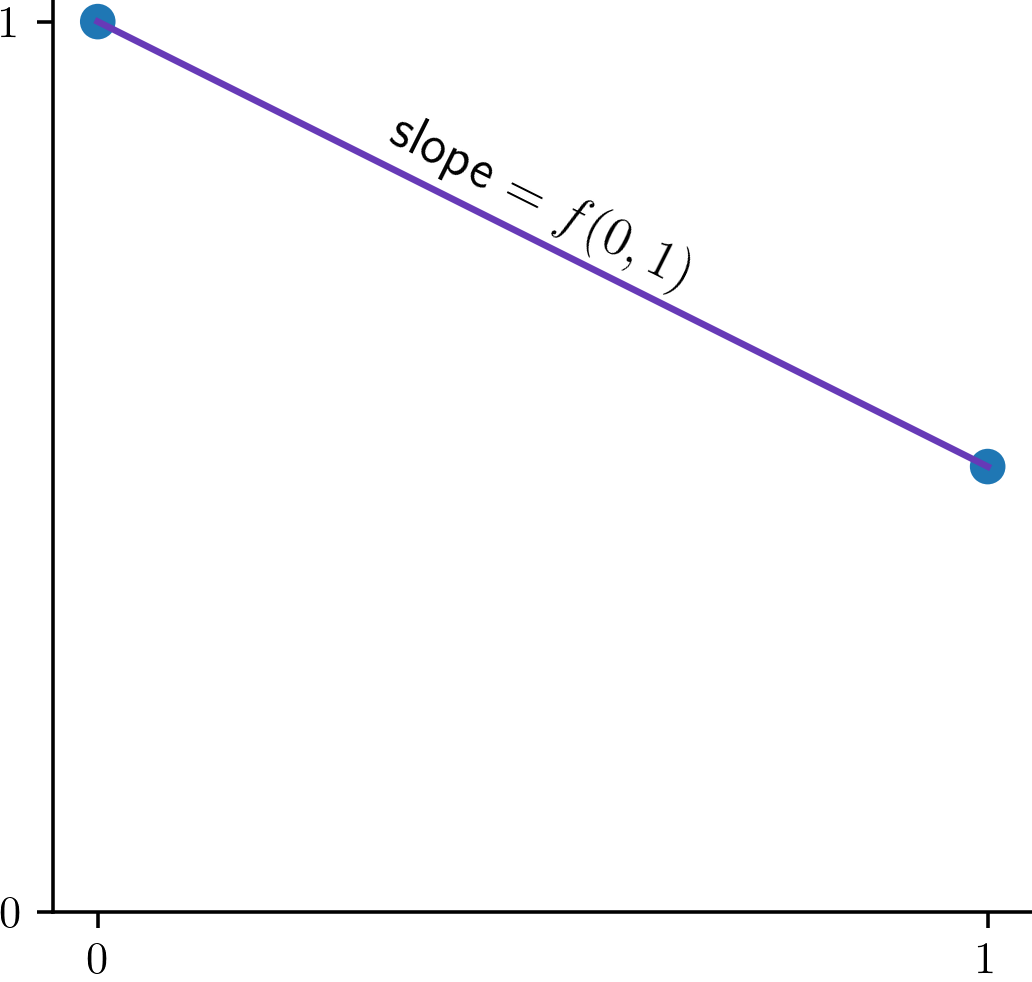
  The line segment will pass through the point $$(1 , \answer {\frac {1}{2}})$$ (use your value of $f(0,1)$ to compute a numerical value of $y$ corresponding to $x = 1$).

• Now we repeat: Take a new line segment beginning at the point you just found.

  

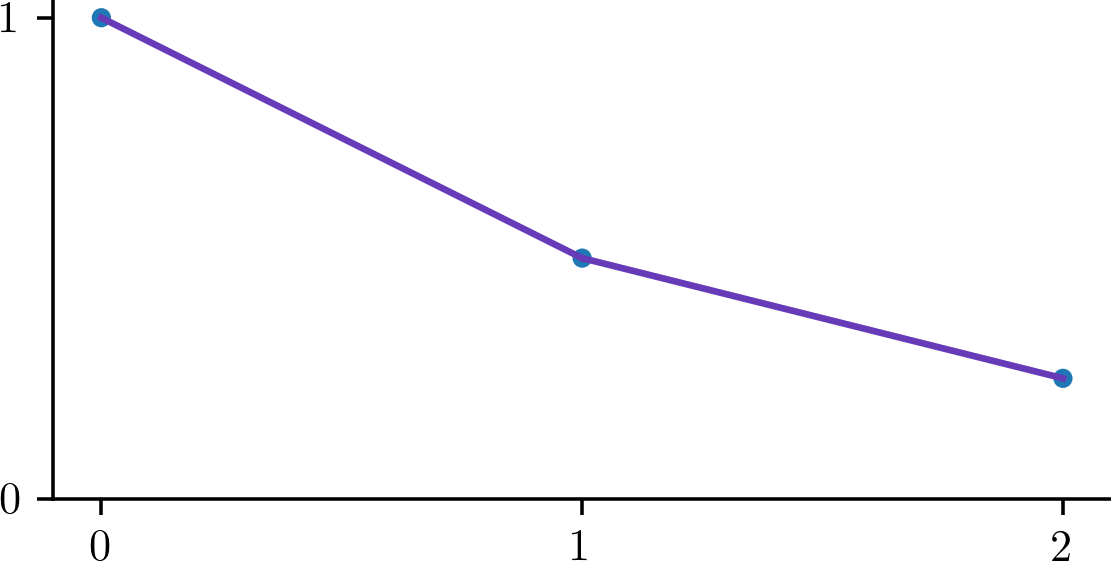
  Its slope is given by $$f \left (1,\answer {\frac {1}{2}} \right ) = \answer {-\frac {1}{4}}.$$ This new line segment passes through the point $(2,\answer {1/4})$.

• Repeat again:

  

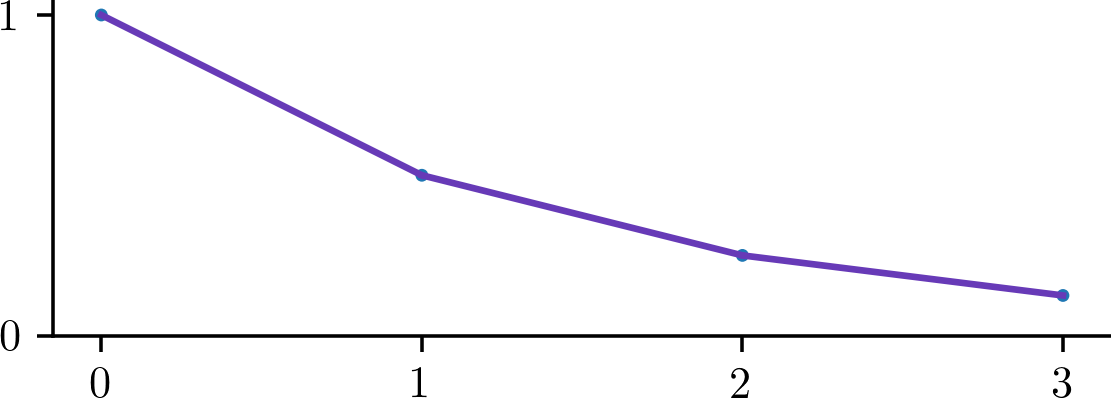
  the line segment beginning at the point you just found will have slope $$f \left (2,\answer {\frac {1}{4}} \right ) = \answer {-\frac {1}{8}}$$ and will pass through the point $(3,\answer {1/8})$. Since we have arrived at an $x$-value of $3$, we may stop. The $y$-value of this most recent point is our answer: $$y(3) \approx \answer {\frac {1}{8}}.$$