Introduction

This course aims to provide you with a background in all the tools you’ll need to be successful in calculus. But what’s the big deal with calculus? Why is it so important? In this section, we’ll provide a brief overview of some of the types of problems you’ll be able to solve with calculus.

Speed

Say you’re running, and the number of miles you run in minutes can be given by . What is your speed at the start of mile 2?

Calculus allows us to talk about instantaneous speeds and rates of change, rather than just average rates of change.

Optimization

Say you want to build a fence, and one side of the fenced-in area is already bounded by a building. If your budget only allows for the purchase of 1000 feet of fencing material, what is the largest area which can be enclosed by the fence?

Calculus can answer many questions about maximizing or minimizing certain values.

Finding Maxima and Minima

When we talked about rational functions and polynomials, there was certain information about their graphs that we couldn’t provide. For example, the graph of the function defined by is shown below.

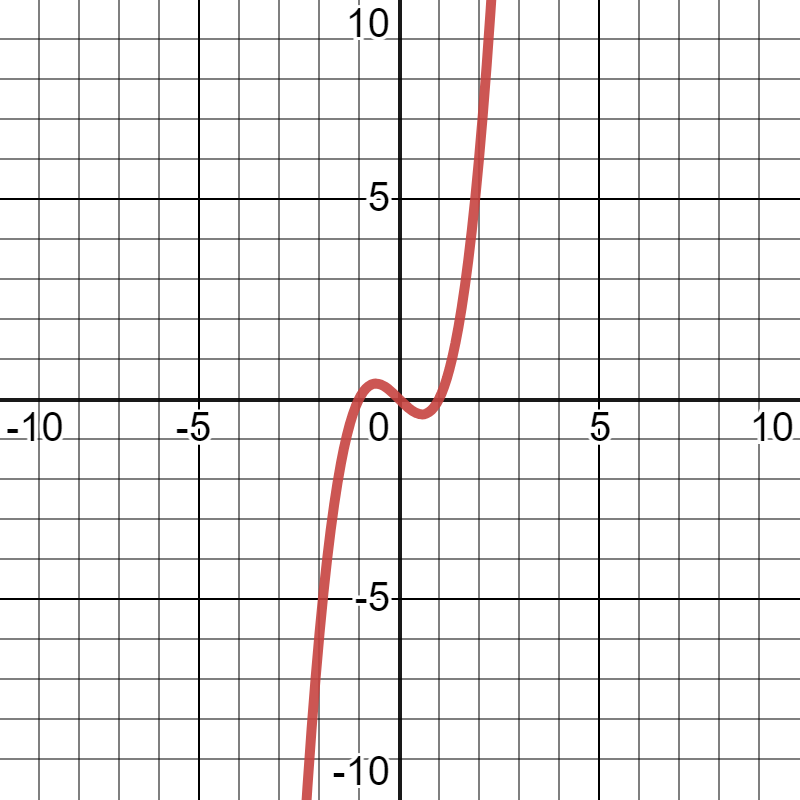
We can answer questions about its end behavior with the concepts learned in this course. However, we notice that there are a peak and a valley on the graph of . Calculus will give us the tools to be able to find the exact location of those points.

Calculus helps us find relative maxima and minima.

Volume of Solids

Say you have a bowl whose silhouette viewed from the side can be described by a parabola. Assume its cross-sections are perfect circles. What is the volume of the bowl?

Calculus can help us find the volume of many different kinds of 3D solids.

Related Rates

Say you’re filling a cone with base radius 100 centimeters and height 100 centimeters with water at a rate of 4 centimeters cubed per minute. How quickly is the depth of water in the cone is changing when the water is at a height of 50 centimeters?

Calculus can allow us to describe rates of change in relation to other rates of change.

Newton’s Method

Say you’re looking at a really complicated function, like . Finding the roots of this function algebraically is impossible, but if you start with a good estimate of the root, a tool from calculus called Newton’s method can refine your solution into a better estimate. What’s more, you can then use Newton’s method on that better estimate to obtain an even better estimate!

Calculus can help us estimate roots of functions.

Approximations

We know that the sine function is extremely complicated. We saw in the section on inverse trigonometric functions, that sometimes, we can rewrite functions involving trig functions in purely algebraic terms. For example, you can show that . However, we haven’t seen a way to rewrite by itself. However, in certain situations, we can come up with an approximation to functions, and this approximation is linear, which is often much easier to work with! There is a famous linear approximation of , but it only works when is very close to zero. Part of calculus will be learning when certain approximations are good substitutes for the actual function.

Also, there’s no reason to stop at linear functions! We can use higher and higher degree polynomials to get better and better approximations of trig functions, as well as other functions.

Calculus can allow us to approximate complicated functions with polynomials, but these approximations are only good for certain values of .

Average Rates of Change

Say you’re driving in an area where the speed limit is 60 miles per hour. If you drive 6 miles in 5 minutes, your average speed is greater than 60 miles per hour, but your speed at any given point on your trip need not be greater than 60 miles per hour: you may slow down and speed up. Is it possible to go 6 miles in 5 minutes without speeding? In other words, if your average rate of change is greater than 60 miles per hour, is it possible for your instantaneous rate of change to be below 60 miles per hour for the entire trip?

Calculus can give us important information on the relationship between average rates of change and instantaneous rates of change.

Finding the Area

In the project this semester, you wrote equations and inequalities that defined the shapes of letters of the alphabet in the plane. However, if you were using these as a font, a reasonable question would be, “How much ink does each letter use?” To answer this question, we need to find the area of each letter. With the tools we have now, this isn’t possible. However, in calculus, you will learn a way to calculate the exact area of each of your letters.

Calculus provides a method for finding the area bounded by curves in the plane.

Rates of Change

One extremely useful topic in calculus is the idea of instantaneous rates of change. We’ve often computed average rates of change in this course, so it’s important to understand the difference.

Imagine you are in a car making the 73-mile trip from Columbus to Dayton. Google Maps says this takes about 1 hour and 8 minutes, so your average speed during the trip would be

However, you aren’t going 64.4 miles per hour for the entire duration of the trip! At stoplights, your instantaneous speed is 0 miles per hour, and on the highway, your instantaneous speed may be higher than 65 miles per hour. Instantaneous speed captures your speed at a precise moment in time, rather than over an interval of time.

Up until now, we have only been able to calculate the average rate of change of a function. Calculus gives us the tools to be able to calculate the instantaneous rate of change. One very important tool is the idea of the limit.

Limits

Consider the function . Calculate the following values. Enter DNE if the value does not exist.

For , .

.

Notice that the function is defined everywhere except at , that is, its domain is . Where the function is defined, though, . Thus, the graph of looks like a line with slope 1 passing through the origin, but with a hole at the origin. It’s reasonable to say then, that as approaches 0, the value of approaches 0. This motivates the idea of limits. Our function is doing something crazy at , but we can still make a statement about what is happening nearby.

Calculus allows us to talk about the behavior of functions near certain points.