For each input, exactly one output

$\newenvironment {prompt}{}{} \newcommand {\todo }[0]{} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\CancelColor }[0]{} \newcommand {\cancelto }[0]{1} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\proj }{\vec {proj}} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[0]{\overrightarrow } \newcommand {\vec }[0]{\mathbf } \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\boldsymbol {\l }} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1}$ $% This file was *autogenerated* from digInForEachInputExactlyOneOutput.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %e51be318e2595e4ca721cf84367767b9% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

We define the concept of a function.

Life is complex. Part of this complexity stems from the fact that there are many relationships between seemingly unrelated events. Armed with mathematics, we seek to understand the world. Perhaps the most relevant ‘‘real-world’’ relation is

the position of an object with respect to time.

Our observations seem to indicate that every instant in time is associated to a unique positioning of the objects in the universe. You may have heard the saying,

you cannot be two places at the same time,

and it is this fact that motivates our definition for functions.

A function is a relation between sets where for each input, there is exactly one output.

If our function is the ‘‘position with respect to time’’ of some object, then the input is

position time none of the above

and the output is

position time none of the above

Something as simple as a dictionary could be thought of as a relation, as it connects words to definitions. However, a dictionary is not a function, as there are words with multiple definitions. On the other hand, if each word only had a single definition, then a dictionary would be a function.

Which of the following are functions?

Mapping words to their definition in a dictionary. Mapping social security numbers of living people to actual living people. Mapping people to their birth date. Mapping mothers to their children.

Since words may have more than one definition, ‘‘relating words to their definition in a dictionary’’ is not a function.
Since every social security number corresponds exactly to one person, ‘‘relating social security numbers of living people to actual living people’’ is a function.
Since every person only has one birth date, ‘‘relating people to their birth date’’ is a function.
Since mothers can have more (or less) than one child, ‘‘relating mothers to their children’’ is not a function.

Mapping people to their birth date is still a function, even though many people have the same birth date. This is an instance of a function in which an output (a birth date) corresponds to many different inputs (people), but this mapping still a function because each input (person) has exactly one output (birth date). Be careful: the only requirement for a function is that each input has exactly one output, not the other way around!

What we are hoping to convince you is that the following are true:

(a): The definition of a function is well-grounded in a real context.
(b): The definition of a function is flexible enough that it can be used to model a wide range of phenomena.

Whenever we talk about functions, we should explicitly state what type of things the inputs are and what type of things the outputs are. In calculus, functions often define a relation from (a subset of) the real numbers (denoted by $\RR$ ) to (a subset of) the real numbers.

We call the set of the inputs of a function the domain, and we call the set of the outputs of a function the range.

Consider the function $f$ that maps from the real numbers to the real numbers by taking a number and mapping it to its cube: $\begin{align*} 1 &\mapsto 1\\ -2 &\mapsto -8\\ 1.5 &\mapsto 3.375 \end{align*}$ and so on. This function can be described by the formula $f(x)=x^3$ or by the graph shown in the plot below:

A function is a relation (such that for each input, there is exactly one output) between sets. The formula and the graph are merely descriptions of this relation.

A formula describes the relation using symbols.
A graph describes the relation using pictures.

The function is the relation itself, and is independent of how it is described.
For example, if $f(x) = x^2$ and $g(u) = u^2$ , like on the previous card, $f = g$ . Even though these are two different formulas, they describe the same relation, so they are equal functions.

Our next example may be a function that is new to you. It is the greatest integer function.

Consider the greatest integer function. This function maps any real number $x$ to the greatest integer less than or equal to $x$ . People sometimes write this as $f(x) = \lfloor x\rfloor$ , where those funny symbols mean exactly the words above describing the function. For your viewing pleasure, here is a graph of the greatest integer function:

Observe that here we have multiple inputs that give the same output. This is not a problem! To be a function, we merely need to check that for each input, there is exactly one output, and this condition is satisfied.

Compute: $\lfloor 2.4 \rfloor \begin {prompt} =\answer {2} \end {prompt}$

Compute: $\lfloor -2.4 \rfloor \begin {prompt} =\answer {-3} \end {prompt}$

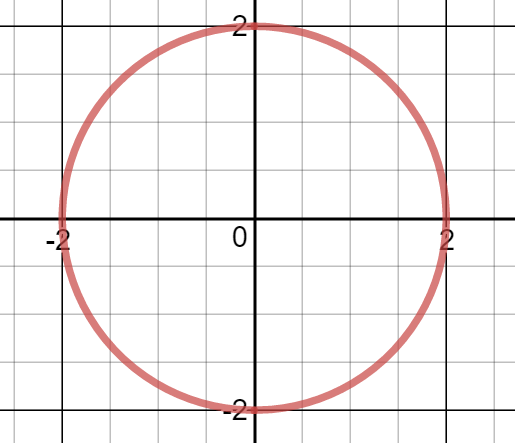
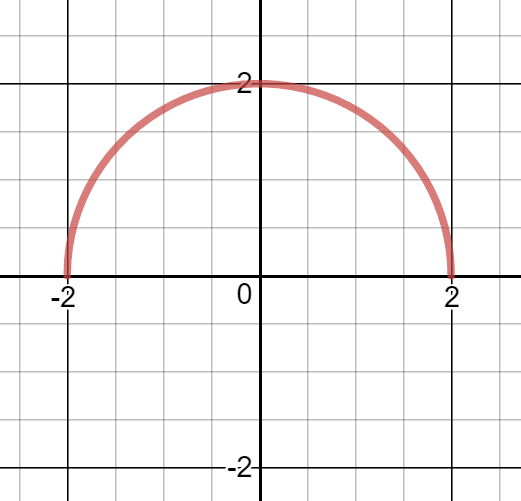
Notice that both the functions described above pass the so-called vertical line test. This test gives a quick visual check of whether each input (or $x$ -value) corresponds to exactly one output (or $y$ value).

The curve $y=f(x)$ represents $y$ as a function of $x$ at $x=a$ if and only if the vertical line $x=a$ intersects the curve $y=f(x)$ at exactly one point. This is called the vertical line test.

To use this test, imagine moving a vertical line over a graph starting on the left and then moving to the right. If there is a vertical line $x=a$ that intersects the graph more than once, then the input, $a$ , corresponds to more than one output (or $y$ -value), so the graph is not the graph of a function. On the other hand, if a vertical line can be moved over an entire graph and always intersects the graph exactly once, then each input corresponds with exactly one output, so the graph is the graph of a function.

Is the graph of the circle $y^2 = 4 - x^2$ shown below the graph of a function?

yes no

Let’s cut the previous circle in half. Is the graph of the semi-circle $y = \sqrt {4 - x^2}$ shown below the graph of a function?

Yes No

Although the circle graph does not represent a function, the graph of the associated semi-circle does. This semi-circle function is called a branch of the circle graph.

Sometimes the domain and range are the entire set of real numbers, denoted by $\RR$ . In our next examples we show that this is not always the case.

Consider the function that maps non-negative real numbers to their positive square root. This function can be described by the formula $f(x) = \sqrt {x}.$ The domain is $0\le x<\infty$ , which we prefer to write as $[0,\infty )$ in interval notation. The range is $[0,\infty )$ . Here is a graph of $y=f(x)$ :

Finally, we will consider a function whose domain is all real numbers except for a single point.

Are $f(x) = \frac {2x}{x} = 2 \cdot \frac {x}{x}$ and $g(x) = 2$ the same function?

Let’s use a series of steps to think about this question. First, what if we compare graphs? Here we see a graph of $f$ :

On the other hand, here is a graph of $g$ :

Second, what if we compare the domains? We cannot evaluate $f$ at $x=\answer [given]{0}$ . This is the only $x$ value where $f$ is undefined, so the domain of $f$ is $\left (\infty , \answer [given]{0}\right ) \ \bigcup \ \left (\answer [given]{0}, \infty \right )$ . On the other hand, there is no value of $x$ where we cannot evaluate $g$ . In other words, the domain of $g$ is $(-\infty , \infty )$ or $\RR$ .

Since these two functions do not have the same graph and they do not have the same domain, they must not be the same function.

However, if we look at the two functions everywhere except at $x = 0$ , we can say that $f(x)=g(x)$ . In other words, $f(x)=2\qquad \text {when}\qquad \text {$x \ne 0$}.$ From this example we see that it is critical to consider the domain and range of a function.