- Do all the trigonometric functions we have seen so far carry the same information?
- How to find all trigonometric functions, given a single one of them?
Introduction
We have encountered six trigonometric functions of an acute angle so far: , , , , , and . They all help up get information about right triangles having as one of the inner angles. But here is the thing: at this stage, they all carry the same information. All of these quantities are positive real numbers, and we have not only the Pythagorean Theorem, but also the fundamental relations
Recall that while the first one is the most important one, the second two are immediate consequences of the first, by dividing it by and , respectively. With all of this in place, once you have one of the six trigonometric values at , you can in fact find all of them. We’ll explore this in this section, with several examples.How to find all trigonometric functions, given one of them?
There are a few main facts one should keep in mind here.
- You know if and only if you know .
- You know if and only if you know .
- You know if and only if you know .
- If you know and , you know .
And there are two strategies: using just the trigonometric identities and proceeding algebraically (let’s call this “strategy 1”), or drawing a suitable right triangle and thinking of , and (let’s call this “strategy 2”). We’ll illustrate both of them with several examples, but at the end of the day, you may choose whichever strategy you’d like (unless specifically instructed otherwise).
- a.
- Given: .
- Strategy 1: Let’s find first, using the first fundamental identity . We have so With this, we have that Flipping the fractions respectively, we obtain
- Strategy 2: We start by drawing the following triangle:
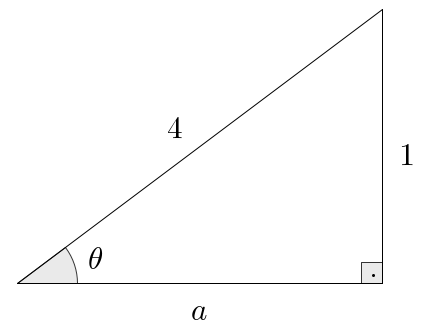
So, we find the missing side , using the Pythagorean relation , which reads and gives: so that . Now we have all the sides, so finding all the ratios is immediate: Flipping all the fractions, we obtain
- b.
- Given: .
- Strategy 1: Let’s find first, using the first fundamental identity . We have so With this, we have that Flipping the fractions respectively, we obtain
- Strategy 2: This time, here’s the triangle we’ll use:
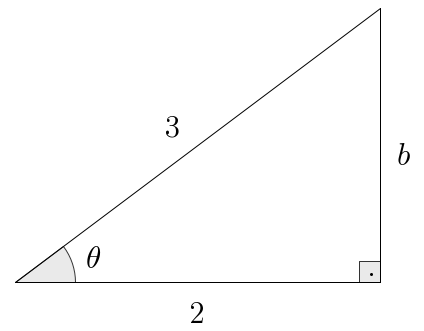
We’ll use the Pythagorean relation to find the missing side , as follows: so . Again, with all the sides, we can read all the main ratios: Taking reciprocals, we get the rest:
- c.
- Given: .
- Strategy 1: The only fundamental identity we have involving is , so we might as well use it. It reads and so With this, we could in principle find , by using as usual. But there is a simpler way. Namely, we use that Meaning that and we are done.
- Strategy 2: Now, we set a right triangle with legs and , like below:
Since the hypotenuse is missing, applying the Pythagorean Theorem is even easier: With this in place, we read from the triangle the main ratios as And taking reciprocals:
- d.
- Given: .
- Strategy 1: We immediately know that , so let’s find next, using the first fundamental identity . We have so With this, we have that Flipping the remaining fractions respectively, we obtain
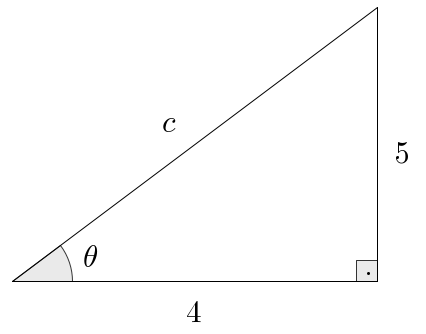
- Strategy 2: Let’s draw a triangle with hypotenuse and adjacent side to
having length :
Let’s use, as usual, the Pythagorean relation to find . It gives us that
So we have that Taking reciprocals and rationalizing each of them, we also get
- e.
- Given: .
- Strategy 1: We immediately know that , so let’s find next, using the first fundamental identity . We have so With this, we have that Flipping the remaining fractions respectively, we obtain
- Strategy 2: Consider the following triangle:
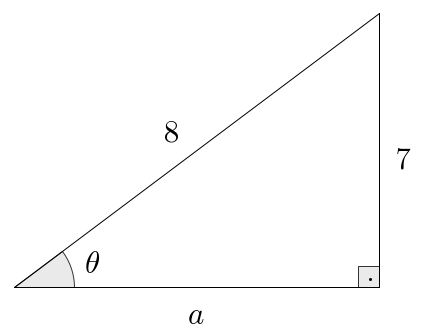
Let’s find using the Pythagorean relation , which becomes so that . Having all the sides of the triangle, we read that Taking reciprocals, we get as well.
- f.
- Given: .
- Strategy 1: We immediately know that and, again, the only
fundamental identity we have involving is . It reads
and so
Again, instead of using to find , we can just argue that
Meaning that
and so we are done.
As an aside, try to solve this problem again without immediately using that . Start only with , use the identity and go from there; it is instructive.
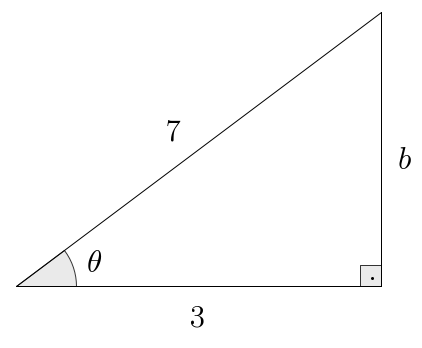
- Strategy 2: Again, let’s set up a convenient triangle:
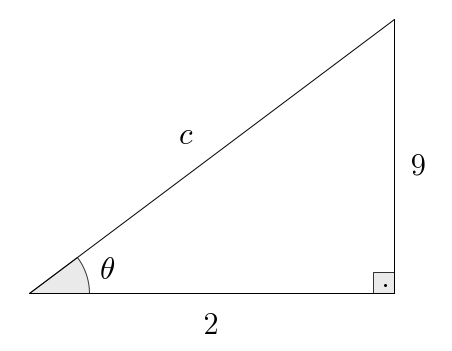
Here, in particular, note that the scale and proportions in this picture are completely off. This is ok, since drawing triangles is just meant to help us organize what is the opposite side to , what is the adjacent side, and what is the hypotenuse. It doesn’t matter how bad your picture looks, as long as the “positions” are correct. In any case, we immediately find with so . Now we can read all the ratios and rationalize them to obtain: Take reciprocals and rationalize whatever is needed to get as well.
- Strategy 1: We immediately know that and, again, the only
fundamental identity we have involving is . It reads
and so
Again, instead of using to find , we can just argue that
Meaning that
and so we are done.
Let’s summarize the highlights of the strategy, from the algebraic perspective.
- (a)
- If you’re given or , use the fundamental identity to find the other one. Then find , and flip all the fractions to get , and .
- (b)
- If you’re given or , flip it to get or , and proceed as (a).
- (c)
- If you’re given , use to find . Once you have , you have . Then proceed as (a).
- (d)
- If you’re given , flip it to get , and proceed as (c).
Note that we’re employing a mathematician’s general philosophy here: take a problem and reduce it to something which you already know how to solve (namely, we’re arguing that — morally — if you know how to solve the problem when you were given either or , then you in fact know how to solve it when given any of the six trigonometric functions). And also from the geometric perspective, the strategy is even easier to describe: recognize the trigonometric function you were given in terms of , and , then draw a right triangle with this information. You will be missing one side, which can be found with the Pythagorean Theorem. Once you have all sides, you can find all the ratios between sides.
Of course, the two above ways to go about this are not the only ones, but they’re as good a recipe as any. In any case, you have room for creativity here. And even if one method seems easier than the other, it is useful to be comfortable with both, as this is already a good chance to start getting acquainted with trigonometry identities, which will be indispensable later.
We will see later how to define and deal with trigonometric functions for angles which are not necessarily acute. Then, everything we did here becomes slightly more subtle, as one must now pay attention to signs (for example, we’ll have that ). But the overall program of using the fundamental trigonometric identities and the relations between the main trigonometric functions (, , and ) with their reciprocals (, , and ) will always be useful.
- We have illustrated, with several examples, two ways to find all the values of the trigonometric functions at an acute angle , once we know one of the values. This can be done algebraically by exploring trigonometric identities, or geometrically by drawing the “correct” triangle and applying the Pythagorean Theorem to find the missing side – to then read all ratios directly from the triangle itself.