977aa5…: “Toward a summer solution”

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\,d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

This exercise gives an example of an important type of contour plot that arises in electrostatics.

The magnitude of force that a particle of charge $Q$ exerts on a particle of charge $q$ that is $r$ units away is given by Coulomb’s Law

$F(r) = \frac {kQq}{r^2},$

where $k =8.99 \times 10^9\unit {N}\cdot \unit {m}^2 /\unit {C}^2$ is Coulomb’s constant.

When several charges are placed near each other, the force that a test particle of charge $q$ experiences is determined by adding the forces that each charged particle exerts on it. The electric field is a “vector field”; to each point $(x,y)$ in the $xy$ -plane, the electric field associates the force vector experienced by the test charge $q$ .

An interesting fact is that this electric field can actually be realized as the gradient of a certain function $V(x,y)$ , called the electric potential via the formula

$\vec {E}(x,y)=-\grad {V}(x,y),$ and a useful way to visualize electric fields to plot the level curves of the electric potential. These level curves are often referred to as equipotential lines.

The contour plot for the electric potential $V(x,y)$ are below shows equipotential lines for an electric field that results from a charge configuration with positive charges at $(1,2)$ and $(0,-2)$ and a negative charge at $(-3,1)$ .

Assume $V(x,y)$ either increases or decreases between contour lines and $V_x(x,y)$ and $V_y(x,y)$ are defined at all points in the picture.

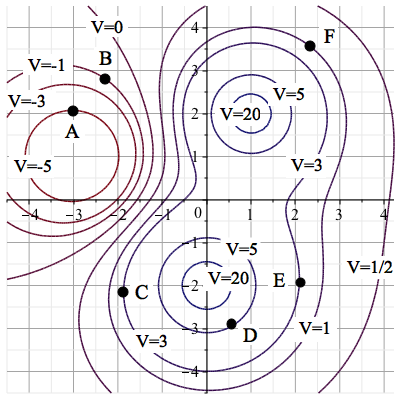
Select all of the points where $V_x(x,y)=0$ .

A B C D E F

Note that the contour plot shows the level curves of the function $V(x,y)$ in the $xy$ -plane, and gives the value that the function takes along them. For instance, the points $C$ , $E$ , and $F$ lie along the level curve associated to $V=3$ .

An important observation is the following.

Since the values of a function do not change along a level curve, the tangent line to a level curve gives the direction in which the instantaneous rate of change of the function is $0$ .

$V_x(a,b)$ is the instantaneous rate of change of the function at $(a,b)$ in the $x$ -direction. Thus, to find the points at which $V_x=0$ , we need to look for the locations where the tangent line to the level curve is in the $x$ -direction. This occurs at point $A$ only.

Select all of the points where $V_y(x,y)=0$ .

A B C D E F

Select all of the points where $V_x(x,y)>0$ .

A B C D E F

To find where $V_x>0$ , we need to look for when the function increases in the $x$ -direction. Since the function either must increase or must decrease between contours, note

We’ve already determined that $V_x =0$ at point $A$ .
As $x$ increases from point $B$ , we move from the contour curve along which $V=-1$ towards the one where $V=0$ . Thus, $V_x>0$ at $B$ .
As $x$ increases from point $C$ , we move from the contour curve along which $V=\answer {3}$ towards the one where $V=\answer {5}$ . Thus, at $C$ .
As $x$ increases from point $D$ , we move from the contour curve along which $V=\answer {5}$ towards the one where $V=\answer {3}$ . Thus, at $D$ .

Select all of the points where $V_y(x,y)<0$ .

A B C D E F