We compute Ramsey numbers in small cases
Ramsey Theory
In this section we consider graph colorings. That is, each edge in a graph will be assigned a particular color. The graph below is a colored with red and blue edges. The vertices represent people and the color represents whether they know each other (red) or not (blue).
The Pigeon Hole Principle suggests that in a with two colors, there must be two of the same color. Hence, in a group of three people, there are at least 2 pairs of people that know each other or two pairs of people that do not.
A fundamental question in Ramsey Theory is: how many people are needed in order to ensure that there is a subgroup of 3 people that are either mutually acquainted or mutually unacquainted? In terms of graphs with edge colorings, what is the smallest value of such that with 2 colors must contain a monochromatic ? This value of is known as a Ramsey Number and denoted
The figure above shows that .
We now prove that .
The smallest number of vertices for which a with edges colored red and blue must
contain a monochromatic is 6, i.e., .
- Proof
- Consider a with edges colored red and blue. We must show that it
contains a monochromatic . Let be any vertex in the . V has 5 edges emanating
from it. By the Pigeon Hole Principle, there must be at least 3 of the same color.
Without loss of generality, assume is connected to vertices and with red edges, as pictured above. Then consider the embedded in the consisting of vertices and . If this contains a red edge, say from to , then the formed by and is monochromatic (red). If the does not contain a red edge, then IT is a monochromatic (blue). Either way, the must contain a monochromatic . Finally, since we can conclude that .
We can use more than two colors. Suppose we use green, red and blue to color the edges of . What is the minimum value of that guarantees a monochromatic ? This Ramsey Number is denoted .
Let be a vertex of with edges colored green, red and blue. There are 16 edges
emanating from . By the Pigeon Hole Principle, there must be at least 6 of one color
(otherwise, we would have at most 5 of each color and 5+5+5 = 15 ¡16).
Which color this is is unimportant, so let’s say it is green. Thus we can
say that the vertex is joined to the vertices by green edges. Now, if any
of the edges connecting an with an are green, then would be a green
and hence the would have a monochromatic as claimed. So now we must
consider the possibility that none of the edges connecting and to any other is
colored green. In this case, all of the edges among the 6 vertices would be
colored either red or blue. Thus we would have a colored with two colors
embedded in our . By the previous theorem, , so we are guaranteed that
this embedded contains a monochromatic . We can now conclude that . To
see that it is actually 17, we must exhibit a coloring of with three colors
that does not contain a monochromatic . The standard example is pictured
below. The three identical monochromatic subgraphs are know as the Clebsch
graph.
Suppose is colored using 4 colors: yellow, green, red and blue. The smallest value of
that guarantees a monochromatic is denoted . Show that
How many edges must emanate from a vertex in to ensure that there are at least 17 of one color?
How many vertices must a graph have to be sure that this many edges emanate from each vertex?
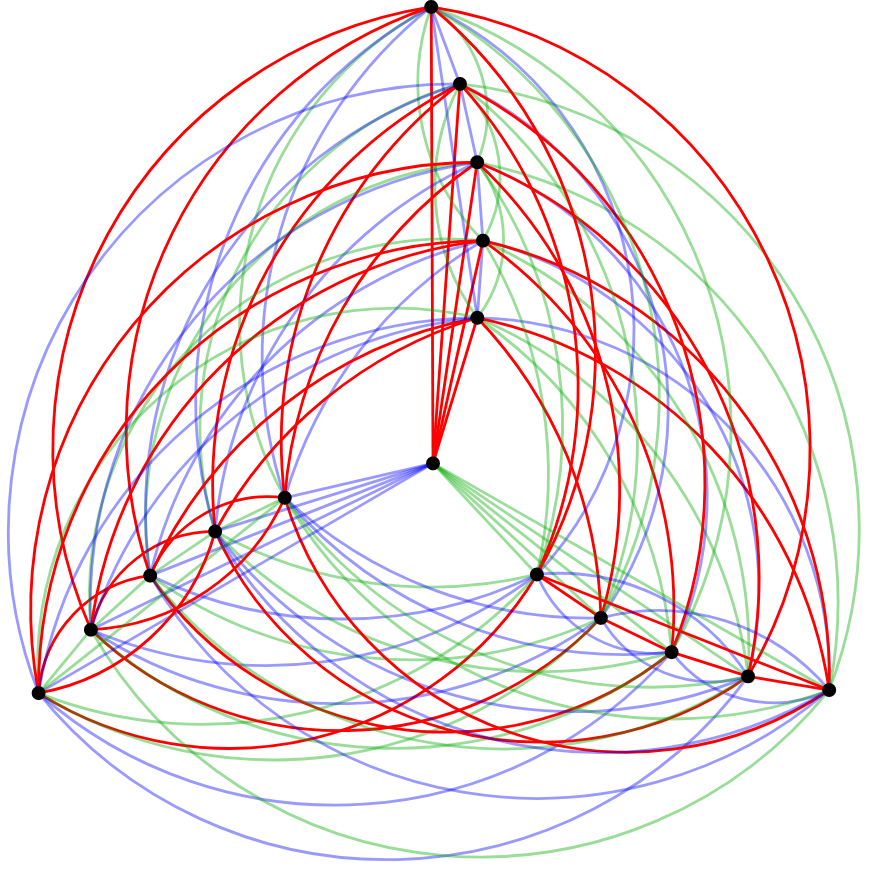
How many edges must emanate from a vertex in to ensure that there are at least 17 of one color?
How many vertices must a graph have to be sure that this many edges emanate from each vertex?