

Photo 1 was taken by
Photo 2 was taken by
Photo 3 was taken by
Group Discussion Prompt: Discuss the reasons for your choices. Do you think it is possible to use these photographs to estimate the height of the camera that took each photo?


Photo 1 was taken by
Photo 2 was taken by
Photo 3 was taken by
Group Discussion Prompt: Discuss the reasons for your choices. Do you think it is possible to use these photographs to estimate the height of the camera that took each photo?

The rails appear to meet at a single point. Do you know what this point is called?
The rails, together with the bottom of each photo, form triangles.
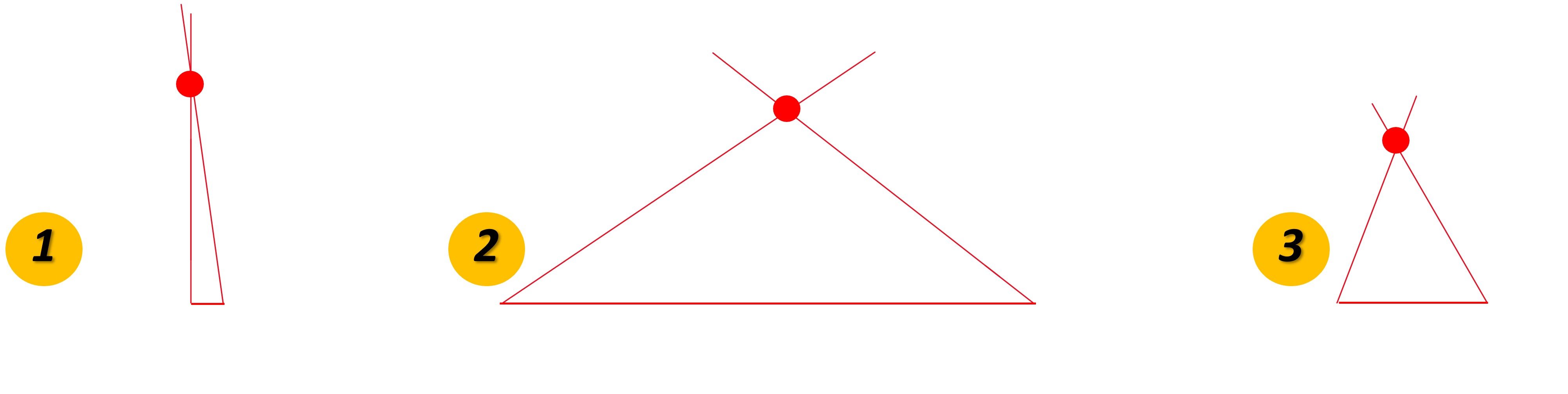
You might describe the first triangle as tall and narrow, and the second triangle as short and wide. These descriptions refer to the proportions of these triangles. To really see the difference in the proportions, we can make the bases of the triangles the same size. This makes sense to do because railroad tracks have the same width everywhere in the U.S.
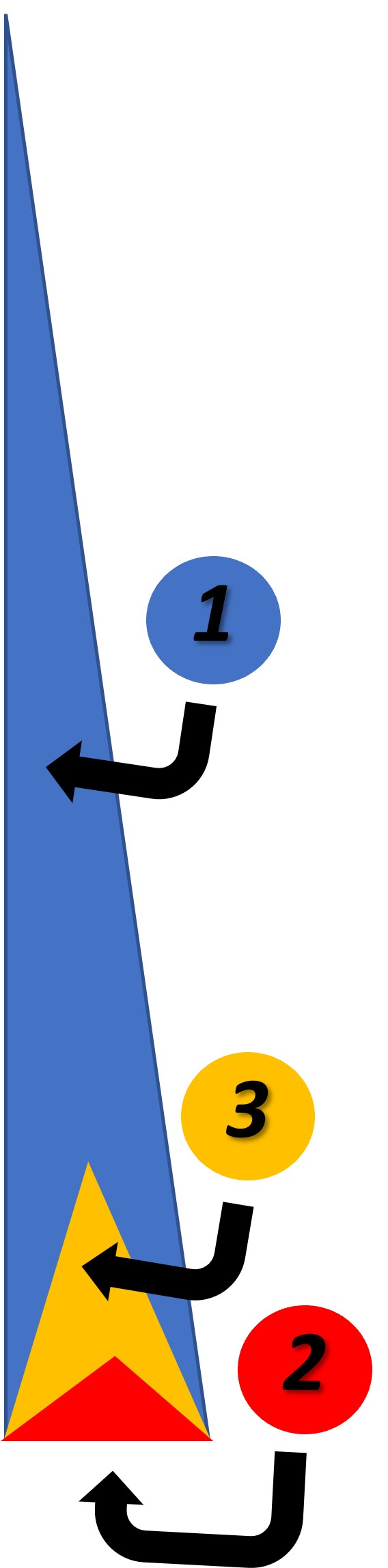
Group Discussion Prompt: In the previous exploration, you figured out who took what photo. Discuss the relationship between the height of the camera and the height of the triangles. Click on the arrow (below, right) for a hint.
Note that Cayla’s triangle (triangle 1) is the tallest, while Adam’s triangle (triangle 2) is the shortest. Recall that Cayla used a drone to take her photo from high above her head.
To see the change in the height of the triangle as the camera height changes, you can use your own phone camera. Find a long hallway or a long table. Position your camera in the middle of the hallway (table). Move the camera up and down observing how the edges of the hallway (table) create taller and shorter triangles, as shown in the photos below.

So far, we have established that there is a relationship between the proportions of the triangle formed by rails (or edges of a hallway), and the height of the camera that took the photo. Next, we will look at a photo for which the measurements of the real-life hallway, and the height of the camera are known. We will numerically relate the proportions of the triangle to the height of the camera.
The following photo shows a -inch wide hallway. The photo was taken with the camera lens inches above the floor.

Observe that the resulting triangle is nearly isosceles. We achieved this by placing the camera as close to the middle of the hallway as we could.
We will now look at the ratio of the height of the triangle to the length of the base.
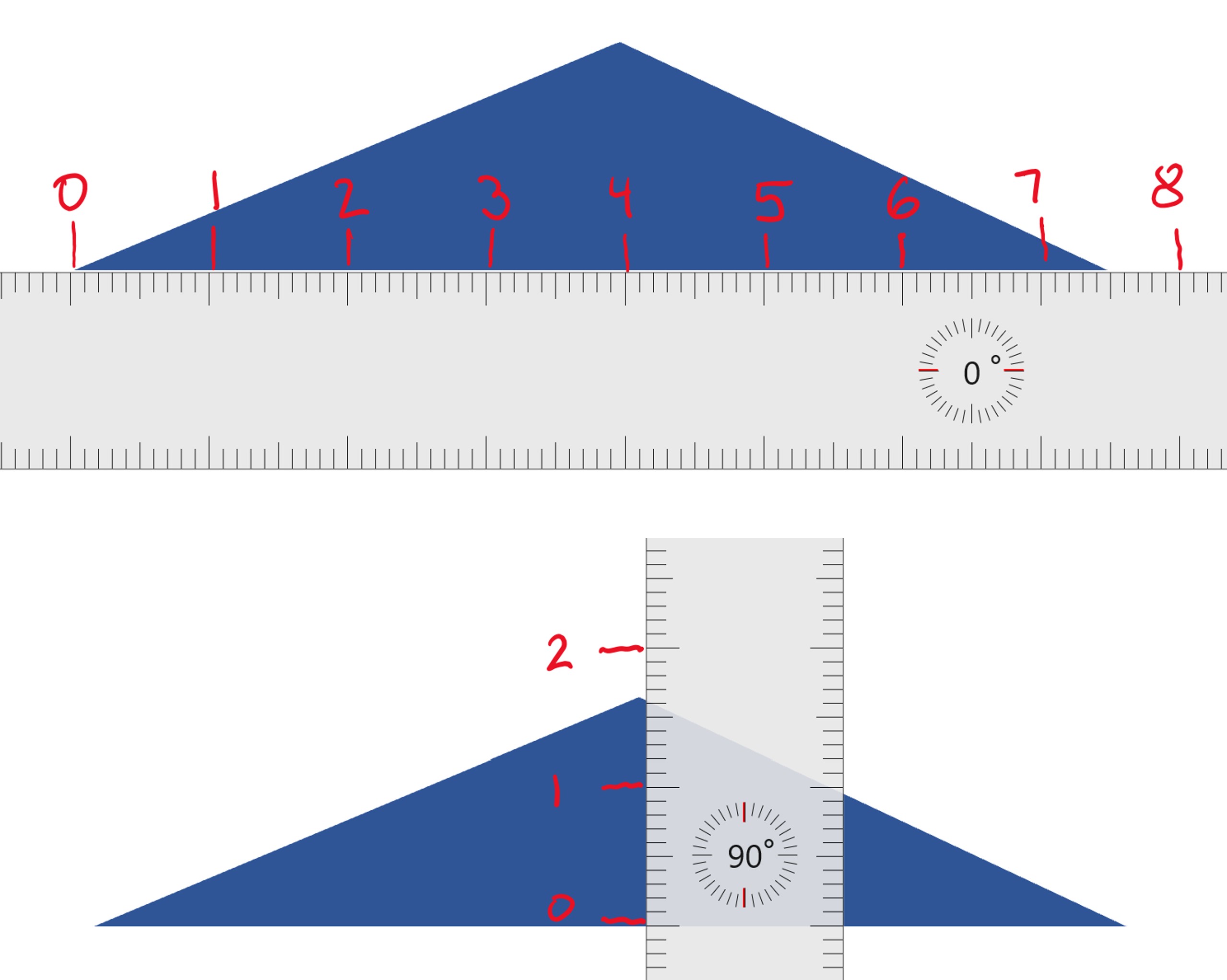
Group Discussion Prompt: Note that our calculations omitted units. Do units matter in this case? If we were to do our measurements using different units, would the ratio still be the same?
Next, we will try to figure out what to do with this ratio to find an estimate for the height of the camera. To do this, suppose we made four prints of our photo. The first print is the size of a small poster, the last print is life-sized. The resulting triangles are clearly of different sizes, but they have the same proportions! Such triangles are called congruent equilateral similarobtuse

Since the last ”print” in the above graphic is life-sized, and the width of the real-life hallway is inches, we can conclude that the base of the last triangle is inches. Set up and solve a proportion to find the height of the last blue triangle.
Compare your answer to the height of the camera given at the start of the problem. The numbers are very close! Do you think this is a coincidence?
Group Discussion Prompt: Formulate a rule for finding the height of the camera for photos with the same set up. How would you verify that your rule works for ALL such photos? Discuss this with your classmates and your teacher.
Group Discussion Prompt: The rule you stated in the previous discussion question is a theoretical rule. In practice, the height of the camera above the floor was given to be inches, but the computed height of the triangle was not exactly . What do you think accounts for the difference?
Group Discussion Prompt: Railroads in the U.S. are built so that the distance between the rails is the same everywhere in the country. The distance between the rails is call the gauge. You can learn more about railroad gauges here. Discuss how you can use this information to find the actual heights that Adam, Benjamin, and Cayla took their pictures from.
In the next two parts of this activity, you will get to perform a photo experiment yourself, and develop the theoretical underpinnings for the rule you discovered here.
Railroad track photos used in this activity were downloaded from WikiMedia Commons.
Photo 1: Dwight Burdette, CC BY 3.0 ¡https://creativecommons.org/licenses/by/3.0¿, via Wikimedia Commons
Photo 2: Antoine Beauvillain, CC0, via Wikimedia Commons
Photo 3: Brian Stansberry, CC BY 4.0 ¡https://creativecommons.org/licenses/by/4.0¿, via Wikimedia Commons
Microsoft clip art was used for student photos.
2024-08-05 16:44:14