When the volume is 10
cubic meters, the depth is 2 meters. As the volume increased from 0 to
10 cubic meters, the depth increased by 2 meters for every cubic meter of
water. When the volume is 10 cubic meters, the depth will increase by 2
meters. As volume varies by a very small amount from 10 cubic meters,
the depth of water increases by 2 times as much as the change in volume.
The instantaneous rate of change of the depth’s value with respect to
volume when the volume is 10 cubic meters is 2 meters per cubic meter.
Please answer each of these questions to the best of your ability. You are welcome to re-watch parts of any of the videos to help you.
Water is flowing into a tank. The function gives the depth of the water in meters
when the volume of the water in the tank is cubic meters. It turns out that .
Which statement best explains the meaning of .
The images below show the graph of a parabola given by . To the right is an image
zoomed in on the point . It turns out that . 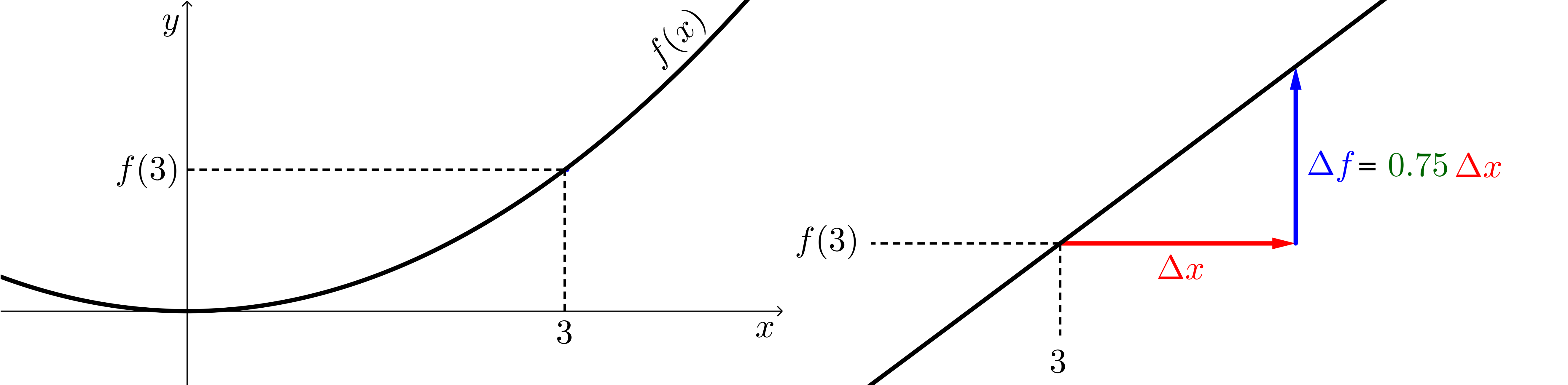 After zooming enough to where the graph of appears essentially linear, which
statement best describes the length of the blue vertical vector?
After zooming enough to where the graph of appears essentially linear, which
statement best describes the length of the blue vertical vector?

The length of the
blue vector is . The length of the blue vector is . The length of the
blue vector is . The length of the blue vector is times as much as the
value of . The length of the blue vector is times as much as the value
of . The length of the blue vector is times as much as the value of .