Three years after purchase, the card’s value is $5. Over the three years after it was purchased, the card’s value increased by $5 every
year. Three years after purchase, the card’s value will increase by $5 over the next
year. As time increases by a very small amount from 3 years, the card’s value
increases by 5 times as much as the change in time. The instantaneous rate of
change of the card’s value with respect to time 3 years after purchase is $5 per year.
To go back to the list of video sets, click HERE.
Before watching the videos, think about and answer these questions to the best of your ability.
The function gives the value of a particular baseball card in dollars where is the
number of years since the card was purchased. It turns out that . Which statement
best explains the meaning of .
The images below show the graph of a logarithmic function given by . To the right is
an image zoomed in on the point . It turns out that .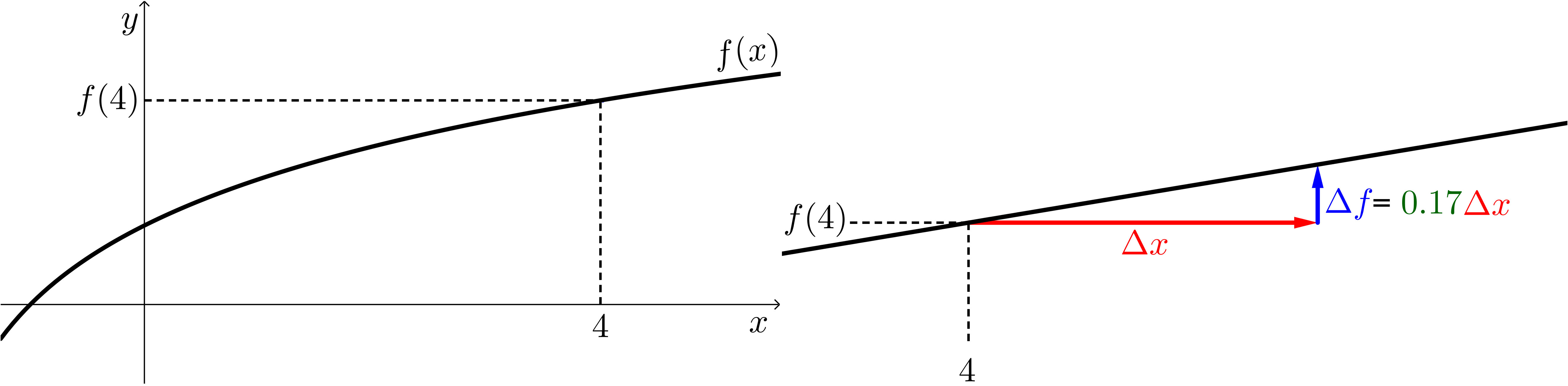 
After zooming enough to where the graph of appears essentially linear, which
statement best describes the length of the blue vertical vector?
The length of the
blue vector is . The length of the blue vector is . The length of the
blue vector is . The length of the blue vector is times as much as the
value of . The length of the blue vector is times as much as the value
of . The length of the blue vector is times as much as the value of .