Parametric plots

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

Tangent and normal vectors can help us make interesting parametric plots.

A sine curve on a circle

Suppose you wish to draw a sine curve on a circle like this:

How do you do this? Well, a general method for placing one curve along another is to use unit tangent and unit normal vectors!

Plot the curve $y= \sin (5x)$ “wrapped” around a circle of radius $3$ .

To do this, start by setting: $\vec {c}(t) = \vector {3\cos (t),\answer [given]{3\sin (t)}}$ The function $\vec {c}$ will draw our circle of radius $3$ . Now we need to add our sine curve. To do this, we compute the unit tangent vector $\begin{align*} \utan(t) &= \frac{\vec{c}'(t)}{|\vec{c}'(t)|}\\ &=\vector{\answer[given]{-\sin(t)},\answer[given]{\cos(t)}} \end{align*}$

and the unit normal vector:

$\begin{align*} \unormal(t) &= \frac{\utan'(t)}{|\utan'(t)|}\\ &=\vector{\answer[given]{-\cos(t)},\answer[given]{-\sin(t)}} \end{align*}$

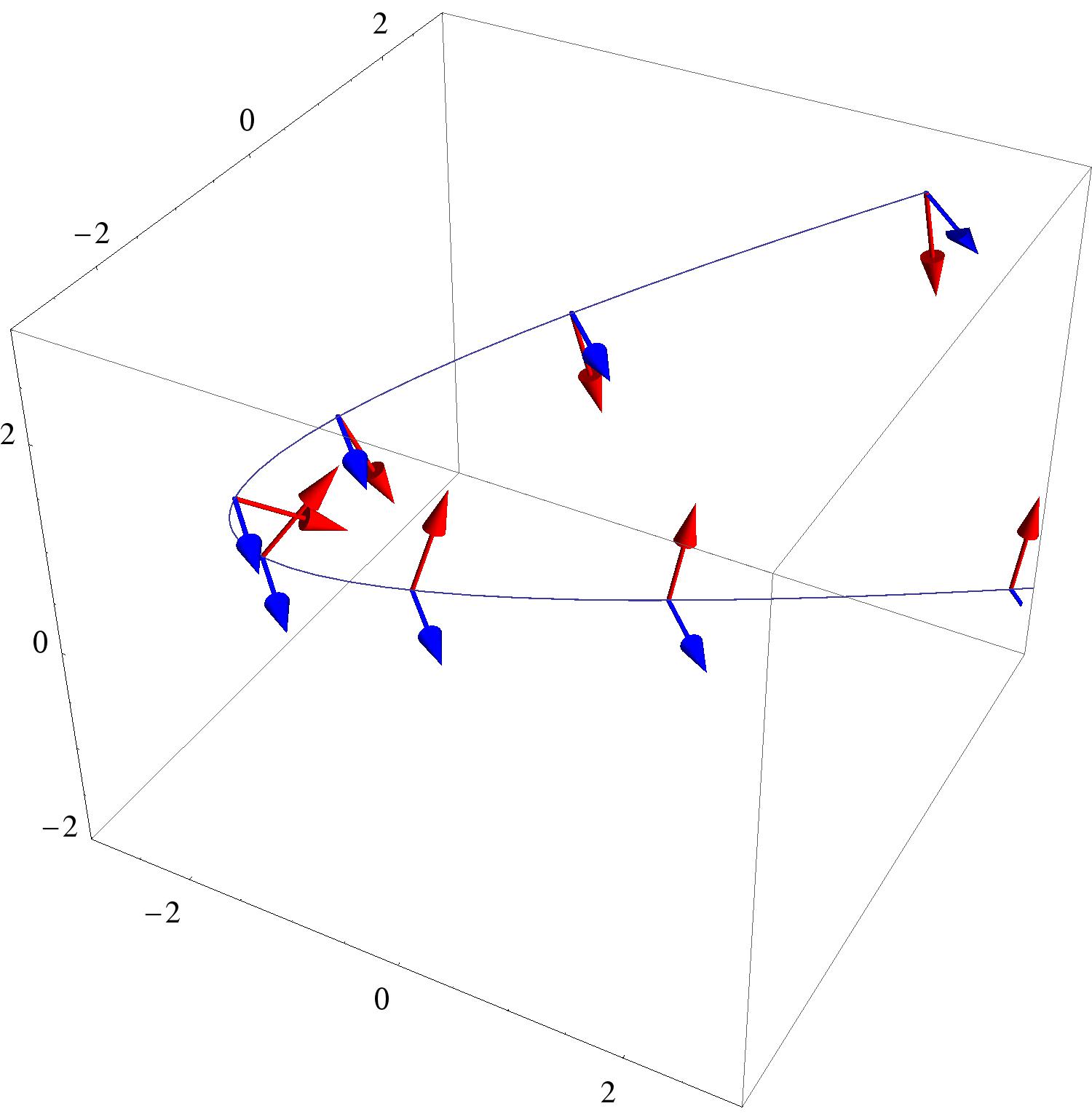
We’ve plotted our circle of radius $3$ with some unit tangent and unit normal vectors for your viewing pleasure:

To add the sine curve, quite literally, add it in: $\vec {f}(t) = \vec {c}(t) + \unormal (t)\cdot \answer [given]{\sin (5t)}$ where $\vec {c}(t)$ draws the circle, and $\unormal (t)\cdot \sin (5t)$ draws the sine curve. Note, breaking $\vec {f}$ in to components we have: $\begin{align*} x(t) &= \answer[given]{3\cos(t)-\sin(5t)\cos(t)}\\ y(t) &= \answer[given]{3\sin(t)-\sin(5t)\sin(t)} \end{align*}$

We can confirm our construction by making a graph:

Thickening a curve

Suppose you have a vector-valued function $\vec {f}:\R \to \R ^2$ that defines a curve in space, and you want to build a parameterized surface that looks like a “thickened” version of the curve. In other words, we want to convert a curve like

into a thickened “tube” like

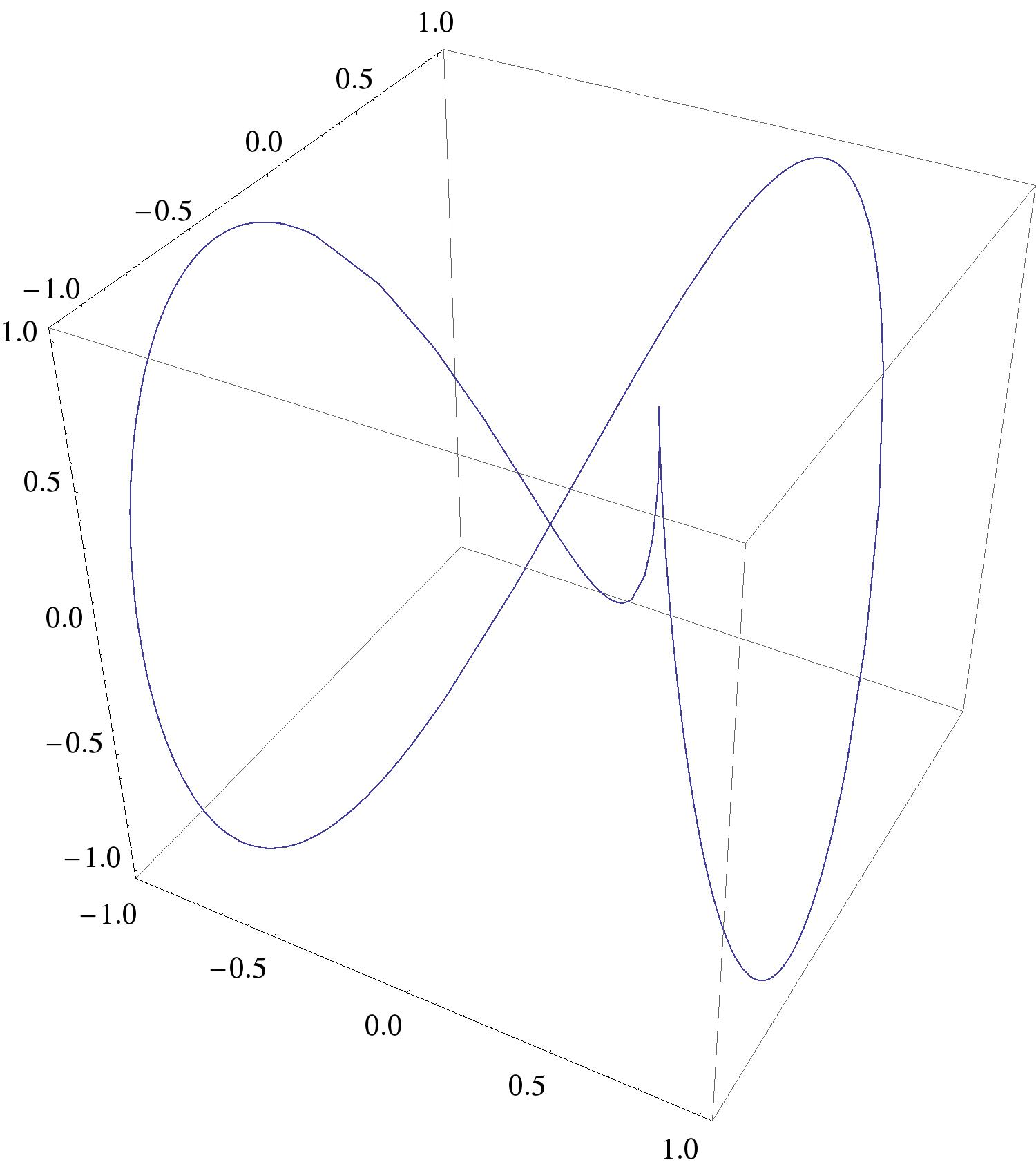
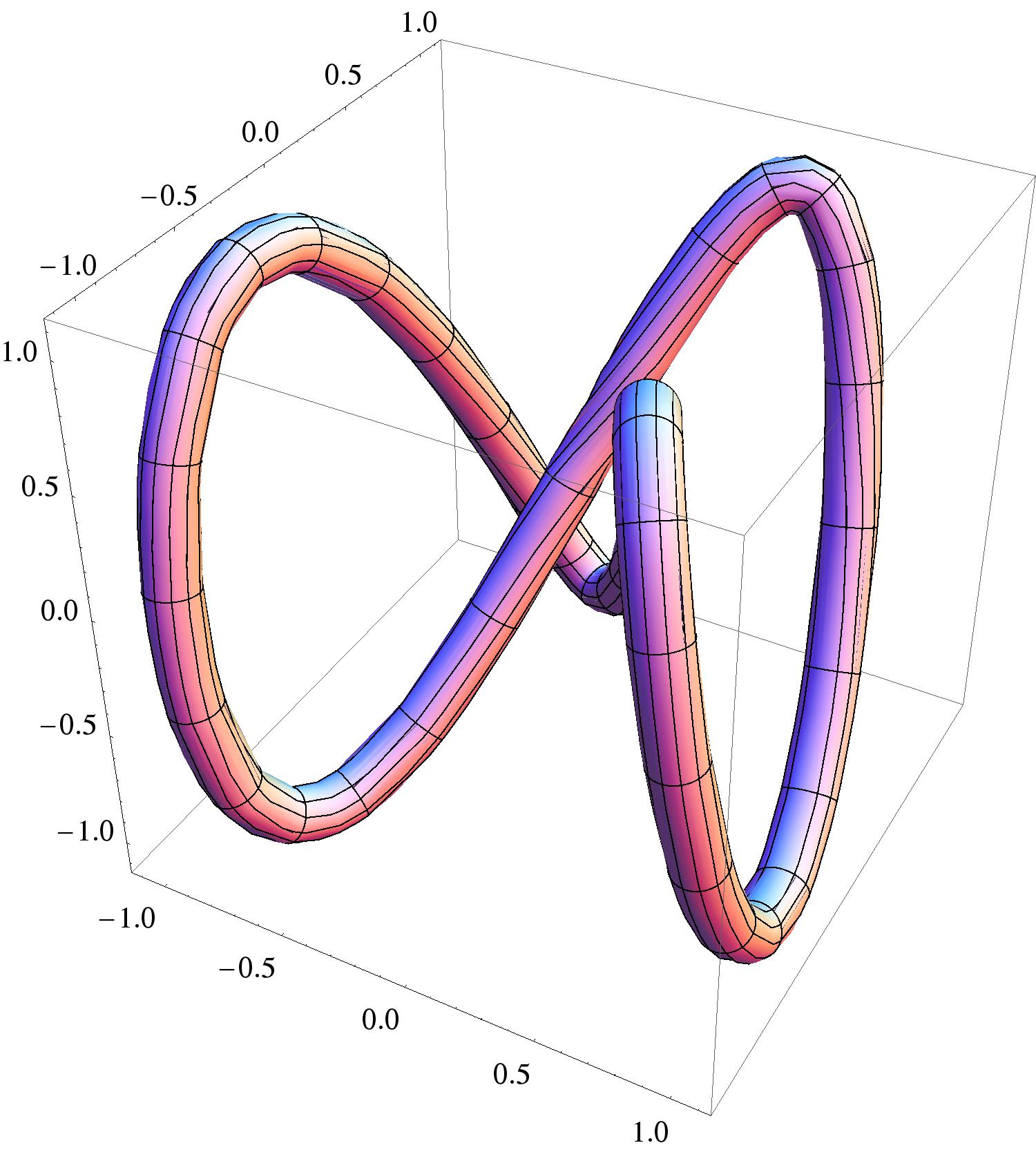
To plot a “tube” around a vector-valued function $\vec {f}$ , we need three handy vectors:

The unit tangent vector: $\utan (t) = \frac {\vec {f}'(t)}{|\vec {f}'(t)|}$
The unit normal vector: $\unormal (t) = \frac {\vec {t}'(t)}{|\vec {t}'(t)|}$
The unit binormal vector: $\ubinormal (t) = \utan (t) \cross \unormal (t)$

Let’s see these vectors in action with our next example.

You have been given a curve in space, say $\vec {f}(t) = \langle t^2-2, t^2-2, 1-t\rangle .$ We want to make a tube around it of radius $0.5$ .

Here is the idea, we want to take our curve and attach two orthogonal vectors to every point

We’ll start by computing the unit tangentunit normalunit binormal vectors. Write with me $\utan (t) = \frac {\vec {f}'(t)}{|\vec {f}'(t)|}$ From these vectors we can obtain the unit tangentunit normalunit binormal vectors by differentiating: $\unormal (t) = \frac {\utan '(t)}{|\utan '(t)|}$ Finally we can obtain the unit tangentunit normalunit binormal vectors via the cross product: $\ubinormal (t) = \utan (t) \cross \unormal (t)$ Looking again at

we see the unit normal vectors in red, and the unit binormal vectors in blue. So we now can plot our tube where $s$ runs from $0$ to $2\pi$ : $\begin{align*} \vec{F}(s,t) = \vec{f}(t) &+ 0.5 \unormal\left(\answer[given]{t}\right)\cos\left(\answer[given]{s}\right)\\ &+ 0.5 \ubinormal\left(\answer[given]{t}\right)\sin\left(\answer[given]{s}\right) \end{align*}$

Here the function $\vec {f}$ runs along the center of the tube, and $\uvec {n}$ and $\uvec {b}$ create a moving axis, where a circle is drawn. Putting this all together we get a tube drawn around $\vec {f}$ . We can check our work with the following interactive: