We develop our quantitative reasoning skills through units, estimations, and asking ‘does that make sense’?
Units
Is 12 the same as 1? As a mathematical value, no 12 and 1 are not the same value.
But if we give these values units, they actually can represent the same thing!
What units can we give to 12 and to 1 so that they are equal?
Within our mathematics and science classes, we often think about units in reference to unit conversion. That is, changing from one unit (such as inches) to another unit (such as feet).
How many inches are in a yard? We might not have this conversion memorized, but if
we know the number of inches in a foot and the number of feet in a yard, we can
figure it out.
There are 12 inches in every 1 foot. This ratio, written as a fraction, is:
There are 3 feet in every 1 yard. This ratio, written as a fraction, is:
Notice these two fractions have foot/feet in common. Let’s use a sketch to help us think about what to do next.
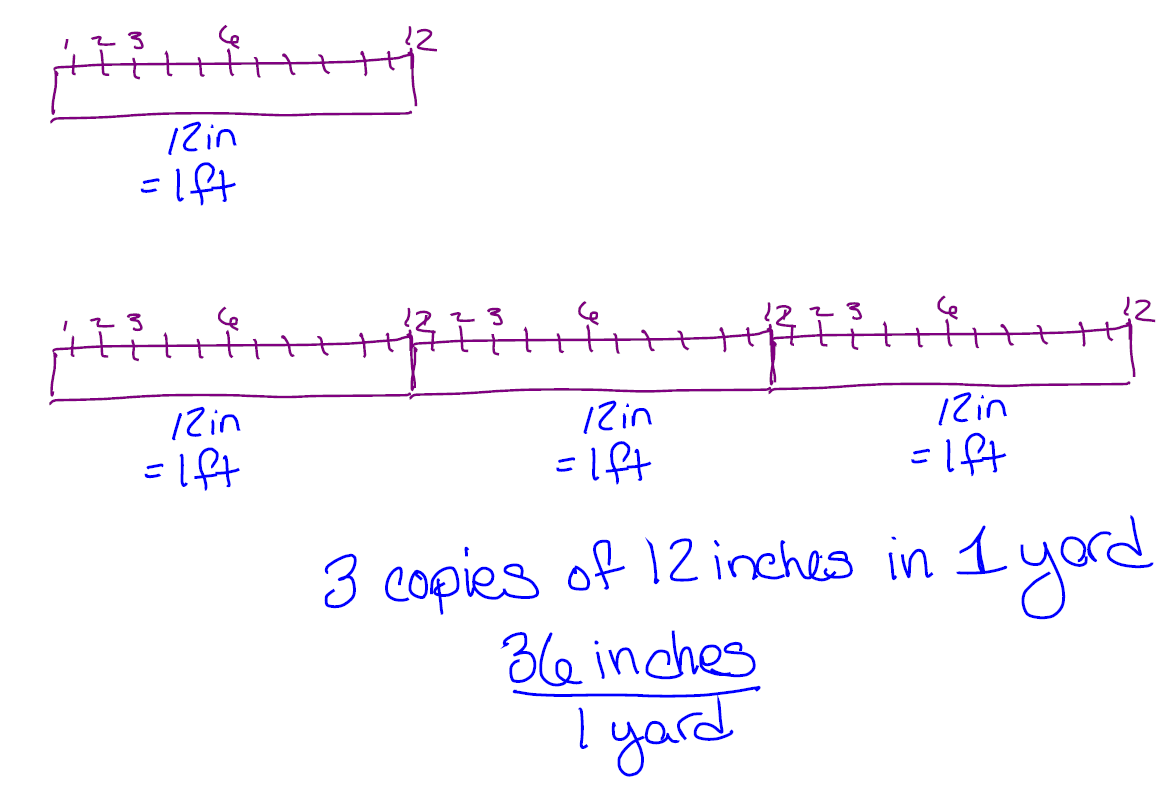
We have a foot ruler comprised of inches. We know there are feet in every yard so we need copies of that ruler to make yard. That gives us rulers of inches each, inches in each yard.
Let’s consider another example.
For each of the questions below, determine if the question makes sense. If it does make sense, find the answer.
- a.
- How many feet are in a square foot?
- b.
- How many square feet are in a square yard?
Let’s look at these questions one at a time.
- a.
- “How many feet are in a square foot?”
This does not make sense. When we’re converting between units, we need to make sure that each of the units is a measurement of the same type. Feet is a measurement in one dimension (length). Square feet is a measurement in two dimensions (area). Cubic feet is a measurement in three dimensions (volume).
- b.
- “How many square feet are in a square yard?”
Let’s draw a picture to help make sense of this. We’ll start by a drawing foot wide by foot tall box. This is a square foot. Now, we know that a yard is feet long so we’ll sketch out a feet wide by feet tall box. This is our square yard. So our question is, how many square foot boxes fit into our square yard box?
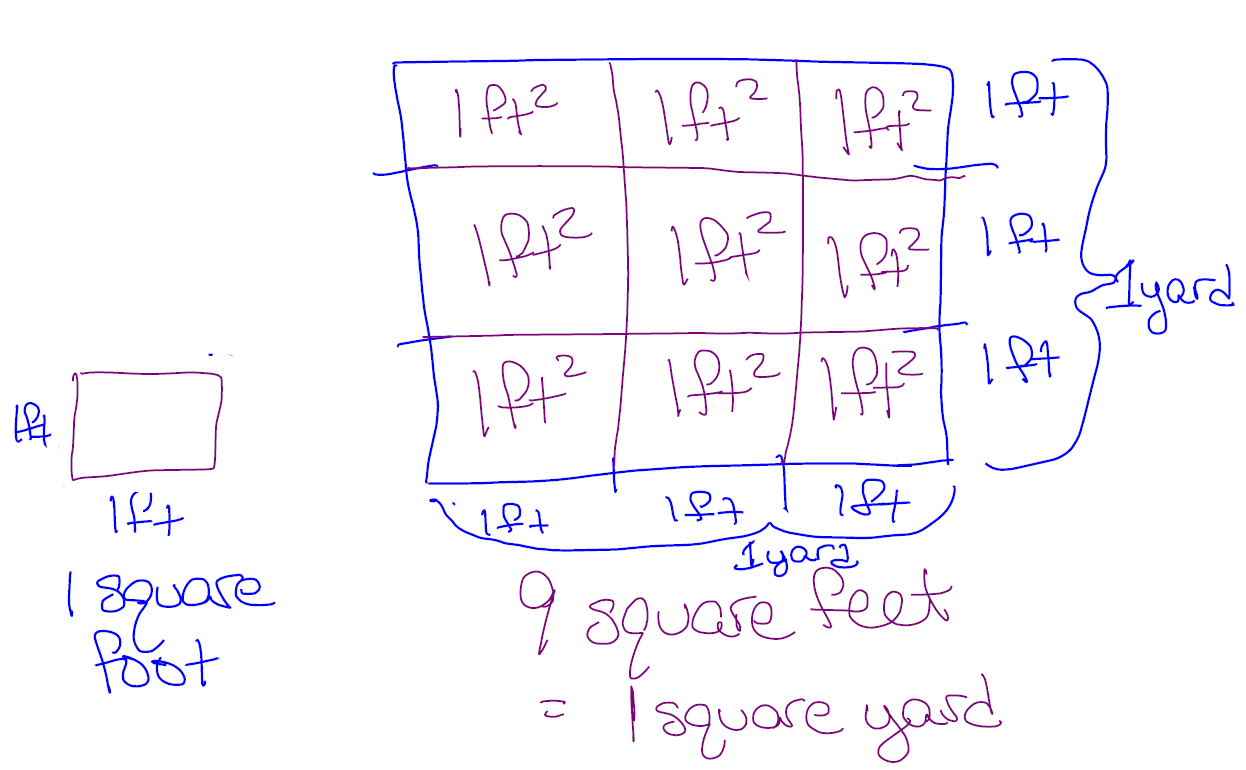
We see that we have square foot boxes that fit into the square yard. There are square feet in a square yard.
Now, its time for you try.
Draw a picture to help you solve the following problem: Peyton is helping Alex move
into their new apartment. The moving truck is yards tall, yards wide, and yards
long. All of the boxes are cubic foot in volume. That is, foot tall, foot wide, food
long. Assuming the boxes fit perfectly into the truck with no gaps, how many boxes
fit into the truck?
We use units everyday, even if we don’t necessarily think of them as units. For example, you wouldn’t say “I went to the grocery store and bought .” what? You’ve given how many you bought (the value), but not how many of what you bought (the units). Instead you would say “I went to the grocery store and bought mangos.” Units help us communicate mathematics, such as numbers, to others.
What if your friend Arjun told you he had calculated that a board for a dog house needed to be cut ? You might scratch your head because feet seems a bit long for the dog house you’re building. Since it doesn’t seem to make sense, you ask Arjun to clarify. He says ‘ inches for the door of the house.’ The units not only conveyed information but also helped to answer the question ‘does that make sense?’
Let’s look at another mathematical tool to help us answer the question ‘does that makes sense?’
Rough Estimates
Rough estimation allows us to approximate the answer to a question without going through messy calculations. For example, Raquel spends $ on matcha tea per week. How much does Raquel spend on matcha tea per year? Rather than do an exact calculation, we can use an estimate. There are many ways to estimate. No one way is correct although some are more accurate than others. For example, we can estimate: OR OR
Why did we multiply? In our first estimate Raquel spends each time she gets matchta tea and she buys matcha tea times a year. So we have groups of .
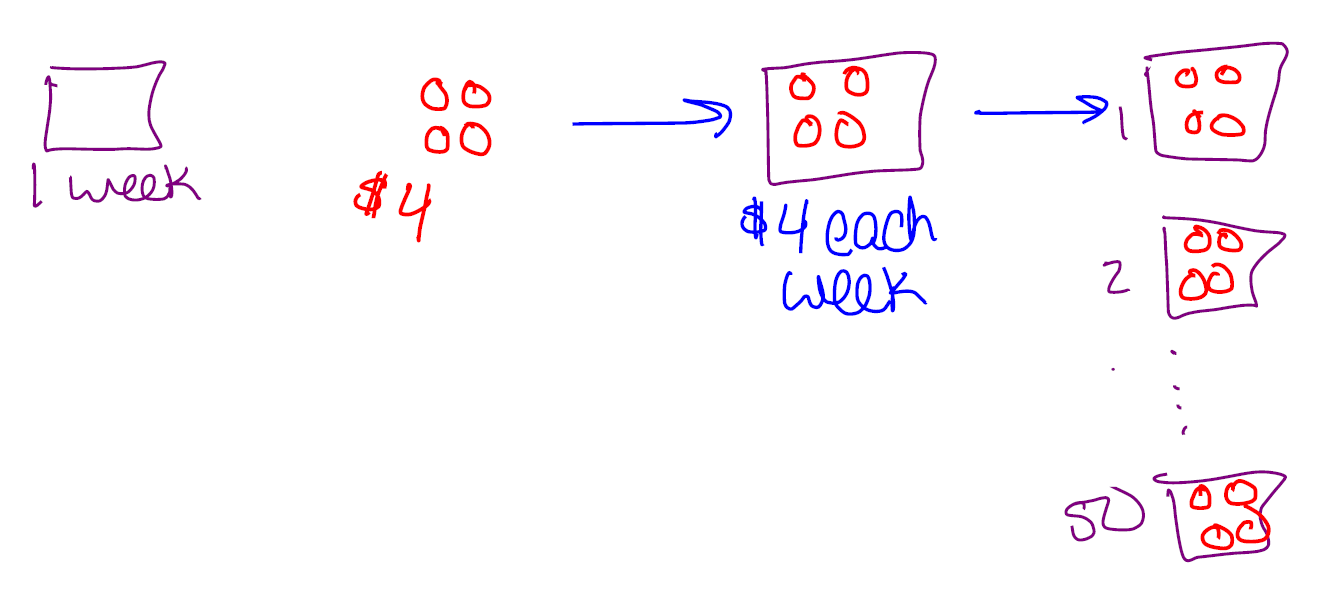
What are the units? The $ may be intuitive but there’s another aspect of units here. In our first estimate, Raquel spends on matcha tea each year. ‘Each year’ helps us answer the question, ‘does that make sense?’ of matcha tea each week seems a bit much. of groceries each year seems like too little. Writing answers down in a sentence helps us reason about our units to then be consider if our answer makes sense. Raquel spends on matcha tea each year.
When we estimate, it’s often important for us to know whether we have overestimated or underestimated. Of the above estimates, $ is an underestimate because we used multiplication and both of the approximate values ( and are less than or equal to the actual values. On the other hand, is an overestimate because and are greater than or equal to the actual values and multiplying two bigger things results in something bigger.
It is very important to remember that rounding up a number does not always result
in an over estimate. For example, if you divide by a number your rounded up, the
resulting answer will actually be smaller! Always think about what operations you
are doing with the numbers when trying to determine if you have an overestimate or
underestimate!
Often the context in which we are estimating will tell us if we prefer to over or under estimate. If Raquel was trying to determine how much to budget for matcha tea for the year, we would want to overestimate the cost to make sure she has enough money. However, what if the question was: Matt earns an hour cleaning houses and he work hours each week. How much money does Matt make per year? Here we want to underestimate the the amount Matt makes so he doesn’t run out of money.
Lets practice by doing an underestimate of how much money Matt makes per year.
Matt earns an hour cleaning houses and works hours each week. Use rough
estimation to find an underestimate for how much money Matt makes per
year.
To underestimate we want to use values that are less than or equal to the given
values because we are multiplying.
- For , depending on how comfortable we are at mental math, we can round down to or use . Both are valid. will give us a more accurate estimate but is easier for mental math.
- For the hours, we can leave that at hours since it’s already a round number.
- For weeks, we can round down to weeks.
We multiply because we have weeks of hours of dollars each hour: OR
Based on our first approximation, Matt earns each year.
Metacognitive Moment Note, if we calculated the money Matt makes per year
using the exact values, we would find he makes
However, technically this is still an estimate. There are many factors we didn’t take
into consideration. For example, taxes, benefits, or unpaid sick time that
come out of wages. The number of days in the year doesn’t divide evenly
into 52 weeks. So some days worked may not be accounted for. In a later
chapter, you’ll learn about mathematical models. When we use math to
explain situations, we have to made decisions about what information to
include.
Let’s try one more example of this type.
Roughly estimate how many gallons of gasoline Li Wei might use to drive from
Columbus, OH to Chicago, IL. The distance to Chicago, IL is about 350 miles
(google maps) and Li Wei’s car gets about 30 miles per gallon (30 miles = 1 gallon)
Explain your answer. Don’t forget units! Also, determine whether your answer is
an overestimate or underestimate and which would be preferrable in this
situation.
Li Wei has to drive miles and for each of those miles, Li Wei’s car will use a gallon
of gas. This question is asking, how many groups of miles fit into miles. This is a
division problem.
If we’re really good at mental math or have a calculator, we can get an exact number of gallons, but an estimate is good enough. Since we need to divide by , let use a numerator that evenly divides by , such as . So now we have:
Li Wei’s car will need approximately 12 gallons of gas for a trip to Chicago, IL.
Now let’s consider whether we have made an overestimate or underestimate. The exact answer would be given by the fraction . Because we increased the numerator of the fraction from to , we made the entire fraction larger. Therefore, our estimate is an overestimate. If we were actually taking a road trip like in this problem, we would want to overestimate the gas we will need so we don’t run out of gas!
Mathematics doesn’t always have one correct answer
As we’ve seen with rough estimations, when problem solving, there can be multiple ways to arrive at an answer. Sometimes, we might choose our round numbers based on ease of comptation, but with other problems, we might choose based on personal preferences. The Pizza Party exploration is an example of this. There’s no one right answer. However, we need to be able to explain our reasoning for our choices and calculations.
Pizza Party: Work with your group to determine what you would buy for a pizza
party in the following scenario. You and your roommate are going to have some
people over later and so you go to the grocery store to grab some snacks. Everyone
has agreed to pitch in $10 to pay for pizza and snacks for the night, and you think
about 12 people are coming over. Your friends will want an account of how the
money was spent so write up an explanation of your reasoning for your choices
and calculations. Here are the prices of various snacks from the grocery
store:
- Bag of tortilla chips - $3.99
- Salsa - $3.79
- Bag of potato chips - $2.99
- Dozen vegan cookies from bakery - $4.99
- Veggie Tray - $14.99
- 12 pack of soda - $5.79
You want to get at least one of each of these items, but you’re also going to order some pizza and breadsticks. Here are the prices from your pizza place:
- Cheese flatbread:
- Medium - $9.99
- Large - $11.99
- Cheese cauliflower crust:
- Medium - $11.49
- Large - $13.49
- Breadsticks:
- 5 for $4.99
- $2.49 delivery charge. Don’t forget tip!
You are a good person and do not plan to pocket any of the money that your friends are going to give you to pay for these pizzas and snacks. Plus, you and your roommate are going to pay for your fairshare (also each pitch in $10). Decide what you’re going to get and don’t forget to write up an explanation of your reasoning for your choices and calculations.