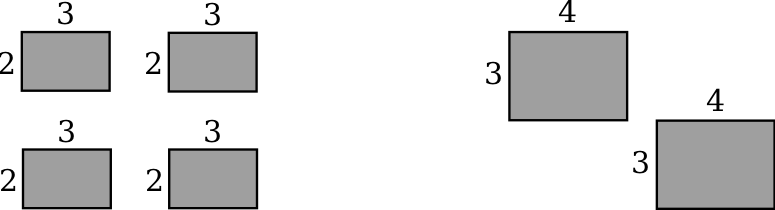Operations and Algorithms

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\framed }[0]{\MakeFramed {\advance \hsize -\width \FrameRestore }} \newcommand {\shaded }[0]{\def \FrameCommand {\fboxsep =\FrameSep \colorbox {shadecolor}}\MakeFramed {\FrameRestore }} \newcommand {\shaded* }[0]{\def \FrameCommand {\fboxsep =\FrameSep \colorbox {shadecolor}}\MakeFramed {\advance \hsize -\width \FrameRestore }} \newcommand {\leftbar }[0]{\def \FrameCommand {\vrule width 3pt \hspace {10pt}}\MakeFramed {\advance \hsize -\width \FrameRestore }} \newcommand {\titled-frame }[1]{\def \FrameCommand {\fboxsep 8pt\fboxrule 2pt \TitleBarFrame {\textbf {#1}}}\def \FirstFrameCommand {\fboxsep 8pt\fboxrule 2pt \TitleBarFrame [$\blacktriangleright $]{\textbf {#1}}}\def \MidFrameCommand {\fboxsep 8pt\fboxrule 2pt \TitleBarFrame [$\blacktriangleright $]{\textbf {#1\ (cont)}}}\def \LastFrameCommand {\fboxsep 8pt\fboxrule 2pt \TitleBarFrame {\textbf {#1\ (cont)}}}\MakeFramed {\advance \hsize -20pt \FrameRestore }} \newcommand {\FrameCommand }[0]{\setlength \fboxrule {\FrameRule }\setlength \fboxsep {\FrameSep }\fbox } \newcommand {\FirstFrameCommand }[0]{\FrameCommand } \newcommand {\MidFrameCommand }[0]{\FrameCommand } \newcommand {\LastFrameCommand }[0]{\FrameCommand } \newcommand {\FrameHeightAdjust }[0]{6pt} \newcommand {\bysame }[0]{\mbox {\rule {3em}{.4pt}}\,} \newcommand {\N }[0]{\mathbb N} \newcommand {\C }[0]{\mathbb C} \newcommand {\W }[0]{\mathbb W} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\Q }[0]{\mathbb Q} \newcommand {\R }[0]{\mathbb R} \newcommand {\A }[0]{\mathbb A} \newcommand {\D }[0]{\mathcal D} \newcommand {\F }[0]{\mathcal F} \newcommand {\ph }[0]{\varphi } \newcommand {\ep }[0]{\varepsilon } \newcommand {\aph }[0]{\alpha } \newcommand {\QM }[0]{\begin {center}{\huge \textbf {?}}\end {center}} \newcommand {\le }[0]{\leqslant } \newcommand {\ge }[0]{\geqslant } \newcommand {\a }[0]{\wedge } \newcommand {\v }[0]{\vee } \newcommand {\l }[0]{\ell } \newcommand {\mat }[0]{\mathsf } \newcommand {\vec }[0]{\mathbf } \newcommand {\subset }[0]{\subseteq } \newcommand {\supset }[0]{\supseteq } \newcommand {\emptyset }[0]{\varnothing } \newcommand {\xto }[0]{\xrightarrow } \newcommand {\qedsymbol }[0]{$\blacksquare $} \newcommand {\bibname }[0]{References and Further Reading} \newcommand {\bar }[0]{\protect \overline } \newcommand {\hat }[0]{\protect \widehat } \newcommand {\tilde }[0]{\widetilde } \newcommand {\tri }[0]{\triangle } \newcommand {\minipad }[0]{\vspace {1ex}} \newcommand {\leftexp }[2]{{\vphantom {#2}}^{#1}{#2}} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\theta }[0]{\vartheta } \newcommand {\l }[0]{\ell } \newcommand {\d }[0]{\,d} \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

Problems about operations and algorithms.

Explain what it means for an operation $\star$ to be associative. Give some relevant and revealing examples and non-examples.

An operation $\star$ is associative if $(a\star b)\star c = a\star (b\star c)$ for all values of $a$ , $b$ , and $c$ . Addition of numbers is associative, as is multiplication. Subtraction and division are not.

Consider the following pictures:

Jesse claims that these pictures represent $(2\cdot 3)\cdot 4$ and $2\cdot (3\cdot 4)$ .

(a): Is Jesse’s claim correct?
Yes. No. Not enough information.
(b): Explain your reasoning.

Jesse is correct. The picture on the left is $4$ copies of $2\cdot 3$ , and the picture on the right is $2$ copies of $3\cdot 4$ .
(c): Do Jesse’s pictures show why multiplication is associative?
Yes. No. Not enough information.
(d): If so, explain why. If not, draw new pictures representing $(2\cdot 3)\cdot 4$ and $2\cdot (3\cdot 4)$ that do show why multiplication is associative.

We can compute that in both cases the total area is $24$ , but that does not explain why they are the same. For that, imagine the volume of a rectangular box measuring $2$ by $3$ by $4$ . Slicing the layers different ways can explain associativity.

Explain what it means for an operation $\star$ to be commutative. Give some relevant and revealing examples and non-examples.

An operation $\star$ is commutative if $a\star b = b\star a$ for all values of $a$ and $b$ . Addition of numbers is commutative, as is multiplication. Subtraction and division are not.

Explain what it means for an operation $\star$ to distribute over another operation $\dagger$ .

An operation $\star$ distributes over an operation $\dagger$ if $a\star (b\dagger c) = (a\star b) \dagger (a\star c)$ and $(b\dagger c)\star a = (b\star a) \dagger (c\star a)$ .

Give some relevant and revealing examples and non-examples.

Multiplication distributes over addition because $a\cdot (b+c) = (a\cdot b)+(a\cdot c)$ and $(b+c)\cdot a = (b\cdot a)+(c\cdot a)$ . But exponentiation does not distribute over addition because $(b+c)\wedge a \ne (b\wedge a)+(c\wedge a)$ .

Explain what it means for an operation $\star$ to be closed on a set of numbers.

A set is closed under an operation $\star$ if for all $a$ and $b$ in the set, $a\star b$ and $b\star a$ are also in the set.

Give some relevant and revealing examples and non-examples.

The counting numbers are closed under addition and also under multiplication but not under subtraction or division. The set of even numbers (including $0$ and negatives) are closed under addition, subtraction, and multiplication. The odd numbers, in contrast, are closed under multiplication but not under addition and not under subtraction.

Sometimes multiplication is described as repeated addition. Does this explain why multiplication is commutative? If so give the explanation. If not, give another description of multiplication that does explain why it is commutative.

Repeated addition by itself does not explain why multiplication is commutative. Organize the repeated addition into an array, interpreting $a\cdot b$ as, say, $a$ rows by $b$ columns. Rotate the array $90^\circ$ , and the array becomes $b$ rows by $a$ columns, or $b\cdot a$ , which must have the same number of objects. Essentially the same reasoning works with an area model.

In beginning algebra, simplifying expressions often involves collecting like terms. But why does this work? Well, the expression $3x+4x$ is equivalent to $(3+4)x$ by the commutativeassociativedistributive property. And then it is clear that $(3+4)x = \answer {7x}$ .

In a warehouse you obtain $20\%$ discount but you must pay a $15\%$ sales tax. Which would save you more money: To have the tax calculated first or the discount? Explain your reasoning—be sure to use relevant terminology. In particular, which property of which operation(s) do you use?

Outline: Build a solution in four steps:

(a): Use a specific starting price.
(b): Generalize the process of computing a price after a discount (assuming no tax).
(c): Generalize the process of computing a price with tax (assuming no discount).
(d): Generalize the two together.

Try a Specific Price. To get started, try a specific starting price, say $\$200$ . Applying the discount first, the price would be $\$\answer {160}$ . After the tax, the cost is $\$\answer {184}$ .

Now try applying the tax first. The original price with tax would be $\$\answer {230}$ . Then with the discount, the cost would be $\$\answer {184}$ , which is greater thanequal toless than the cost when applying the discount first.

Will this work for any starting price? We need to generalize.

Apply a Discount. Suppose the starting price is $\$p$ . A $20\%$ discount, in terms of $p$ , will be $\$\answer {0.2p}$ . So the price after the discount would $p - 0.2p$ . And by the commutativeinversedistributive property, this is equal to $(1-0.2)p$ , or $\answer {0.8p}$ . In other words, rather than computing the discount and subtracting, we can directly compute the new price by multiplying the original price by $\answer {0.8}$ . This makes sense because with a discount of $20$ percent, the price we pay will be $\answer {80}$ percent of the original price.

Apply a Tax. Again, suppose the starting price is $\$p$ . A $15\%$ tax, in terms of $p$ , will be $\$\answer {0.15p}$ . So the price with tax would $p + 0.15p$ . And by the commutativeidentitydistributive property, this is equal to $\answer {1.15p}$ . In other words, rather than computing the tax and adding, we can directly compute the new price by multiplying the original price by $\answer {1.15}$ . This makes sense because with a tax of $15$ percent, the price we pay after tax will be $\answer {115}$ percent of the original price.

Apply both. Again, let the starting price be $\$p$ .

If we apply the discount and then the tax, we multiply $p$ first by $\answer {0.8}$ and then by $\answer {1.15}$ , resulting in the expression $\answer {1.15\cdot 0.8p}$ .

If, on the other hand, we apply the tax and then the discount, we multiply $p$ first by $\answer {1.15}$ and then by $\answer {0.8}$ , resulting in the expression $\answer {0.8\cdot 1.15p}$ .

These expressions are equal because of the identityassociativedistributive and commutativeinversedistributive properties of additionsubtractionmultiplicationdivision . Thus, the final cost is the same either way.

Money Bags Jon likes to give a tip of $20$ % when he is at restaurants. He does this by dividing his bill by $10$ and then doubling it. Explain why this works.

Because $10\%$ is the same as $1/10$ of the bill, and $20\%$ is twice that.

Regular Reggie likes to give a tip of $15$ % when he is at restaurants. He does this by dividing his bill by $10$ and then adding half more to this number. Explain why this works.

Because $10\%$ is the same as $1/10$ of the bill, $5\%$ is half that, and $15\%$ is the same as $10\% + 5\%$ .

Wacky Wally has a strange way of giving tips when he is at restaurants. He does this by rounding his bill up to the nearest multiple of $7$ and then taking the quotient (when that new number is divided by $7$ ). Explain why this isn’t as wacky as it might sound.

If the bill is already a multiple of $7$ , then $1/7$ of the bill is about $14.3\%$ , which is slightly less than a standard tip of $15\%$ . By rounding up to the nearest multiple of 7, the tip will alway be at least $14.3\%$ and usually slightly more.