Circles

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Introduction

In class we studied Riemann sums to find the area under the graph of a function. Recall the following fact:

For a positive function $f(x)$ the area under of the graph of the function is given by $A = \lim _{n \to \infty } \sum _i^n f(x_i) \Delta x$

In this module, you will expand your understanding of Riemann sums with an application to the unit circle. Consider the area of the unit circle, which you know to be $A = \pi r^2 = \pi$ . We will approximate this area (the value of $\pi$ ) by inscribing and circumscribing polygons.

The following video will prepare you for the activity.

Activity

As stated in the video, our goal will be to approximate the value of $\pi$ . We will break this down into individual steps.

Section 1

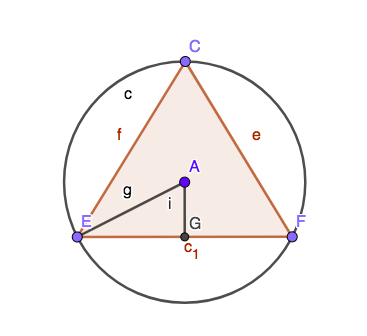
Use the following figure for the questions in section 1. Assume that circle $A$ is a unit circle and that $\overline {AG}$ hits $\overline {EF}$ at a right angle.

Figure 1: Inscribed triangle

The area of the inscribed triangle is less thanequal togreater than the area of the circle.

We will now find the area of $\triangle CFE$ .

What is the length of $\overline {AE}$ ? $\answer {1}$

What is the measure of $\angle AGE$ ? $\answer {90}$ degrees

What is the measure of $\angle EAG$ ? $\answer {60}$ degrees

Use symmetry of the triangle to think about what fraction of a full circle this angle makes.

What is the measure of $\angle AEG$ ? $\answer {30}$ degrees

What is the length of $\overline {AG}$ ? $\answer {.5}$

What is the length of $\overline {EF}$ ? $\answer {\sqrt {3}}$

What is the area of $\triangle CFE$ ? $\answer {3\sqrt {3}/4}$

What is the area of $\triangle AFE$ ? What fraction of $\triangle CFE$ is this smaller triangle?]

Section 2

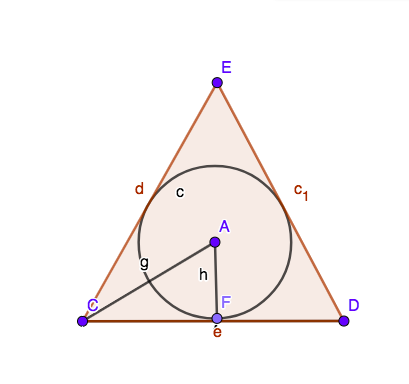
Use the following figure for the questions in Section 2. Again, assume circle A is a unit circle and that $\overline {AF}$ intersects $\overline {CD}$ at a right angle.

Figure 2: Circumscribed/outer triangle

The area of $\triangle EDC$ is less thanequal togreater than the area of the circle.

Which of the following segments have length 1? Select all that apply:

$\overline {AC}$ $\overline {EC}$ $\overline {AF}$ $\overline {CF}$

What is the area of $\triangle EDC$ ? $\answer {3\sqrt {3}}$

Use a similar method as for the inscribed triangle by finding angle measures and then using trigonometry to find side lengths

Using the areas you’ve found, write an interval containing the value $\pi$ . $\answer {3\sqrt {3}/4} < \pi < \answer {3\sqrt {3}}$

Section 3

We will now increase the number of sides in our polygon

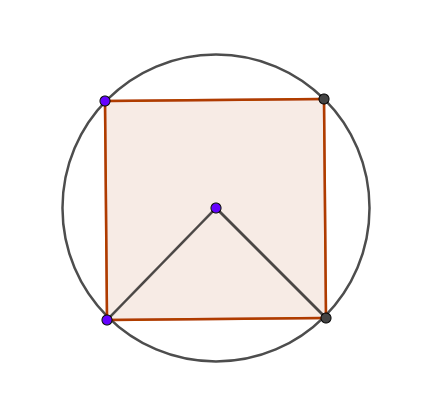
Find the area of a square inscribed in a unit circle. It may be helpful to draw the square and circle. $\answer {2}$

Consider the triangle drawn into the inscribed square below and note that this is an isosceles right triangle (Why?). What are the side lengths of the legs of this triangle? How does that help you find the length of a side length of the square?

Figure 3: Inscribed square

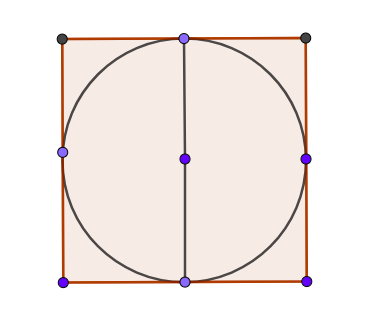
Find the area of a square circumscribed around a unit circle. It may be helpful to draw the square and the circle. $\answer {4}$

How does the radius relate to the side length of the square?

Figure 4: Circumscribed/Outer square

Use the values found in your calculations for the area of a square to refine your bounds on $\pi$ . $\answer {2} < \pi < \answer {4}$

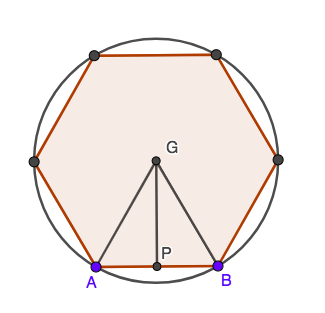
Again increasing the number of sides! To make trigonometric calculations easier, we’re going to skip over the pentagon and work with a hexagon instead.

Use areas of inscribed and circumscribed hexagons to refine your interval further $\answer {3\sqrt {3}/2} < \pi < \answer {2\sqrt {3}}$

Figure 5: Inscribed

Figure 6: Circumscribed/Outer

Figure 7: Hexagons

Consider the diagrams above and try to find the area of the triangle. What fraction of the entire hexagon is this triangle? Recall that radii of the circle have length 1. Can you find any angles in these triangles by considering what fraction of a full circle the top angle is?

Imagine continuing this process. Let $A$ be the area of the unit circle and let $I_n$ be the area of an inscribed n-gon and $O_n$ be the area of a circumscribed (outer) n-gon. Select all that are true:

There exists some very large number $n$ such that $I_n = A$ . There exists some very large number $n$ such that $O_n = A$ . $\lim _{n \to \infty } I_n = A$ $\lim _{n \to \infty } O_n = A$ $\lim _{n \to \infty } I_n = \lim _{n \to \infty } O_n$

Here is something to think about. Can you find formulas for $I_n$ and $O_n$ (as in question 17) in terms of $n$ ? Your answer will need to incorporate trigonometric functions.

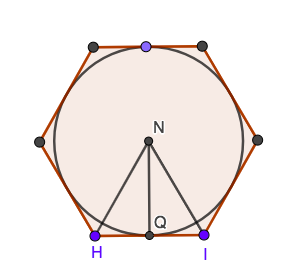
View the image of the inscribed/circumscribed hexagons as in the hint for question 16, but imagine these hexagons to be n-gons. We will be using the same labeling to picture the corresponding triangles formed from one side of the n-gon. Starting with the inscribed n-gon. $\overline {GA}$ is a radius of the circle, hence has length one. We will find the area of $\triangle APG$ , which is $\frac {1}{2n}$ the area of the entire n-gon. $\angle AGP$ has measure $\frac {1}{2n}$ . So the length of $\overline {GP}$ is $\cos (\frac {360}{2n})$ and the length of $\overline {GP}$ is $\sin (\frac {360}{2n}).$ Hence A $(\triangle APG) = \frac {1}{2}\cos (\frac {360}{2n})\sin (\frac {360}{2n})$ and the area of the n-gon is $I_n = n\cos (\frac {360}{2n})\sin (\frac {360}{2n})$ . Now for the circumscribed n-gon. Here $\triangle NQH$ is still $\frac {1}{2n}$ the area of the n-gon. $\overline {NQ}$ has length 1, so length $\overline {QH} = \tan (\frac {360}{2n})$ , implying that A $(\triangle NQH) = \frac {1}{2}\tan (\frac {360}{2n})$ and the area of the n-gon is $O_n = n\tan (\frac {360}{2n})$ .

So we have bounds for $\pi$ : $n\cos (\frac {360}{2n})\sin (\frac {360}{2n}) < \pi < n\tan (\frac {360}{2n})$ .