9.2: Direction Fields and Euler’s Method

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following videos which recap the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

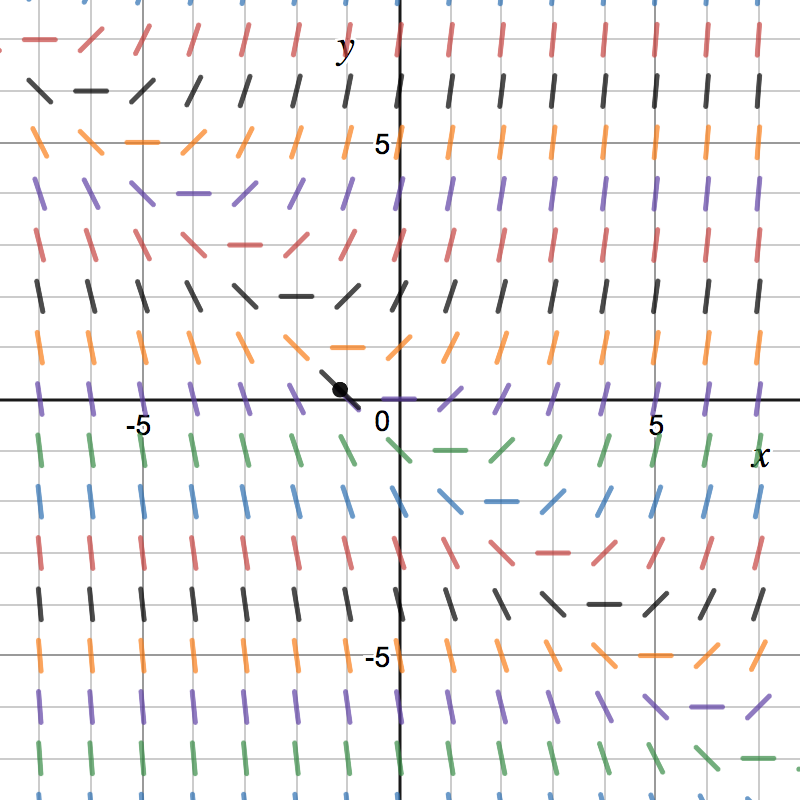
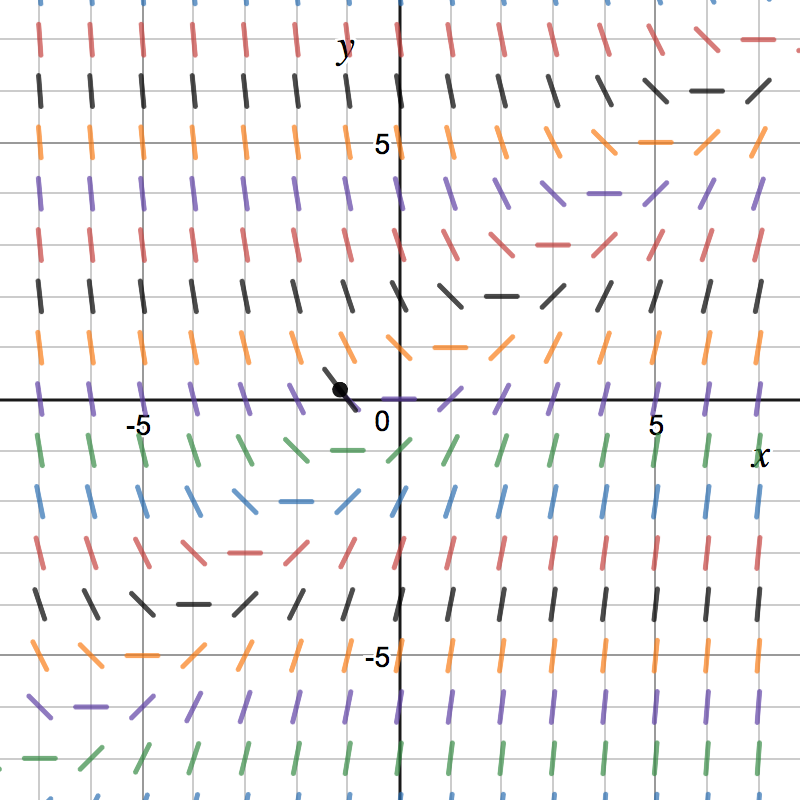
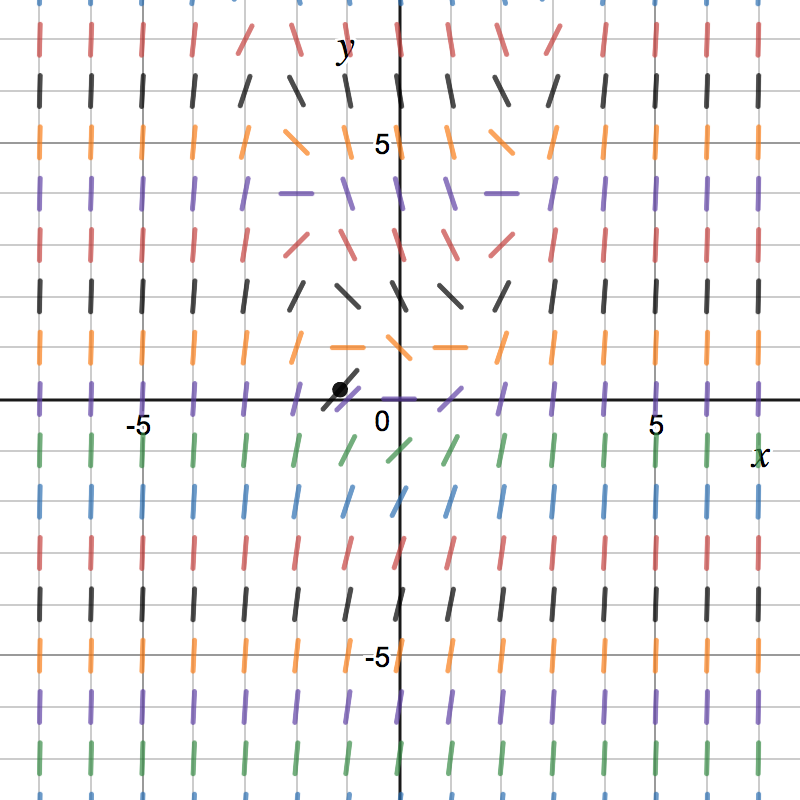
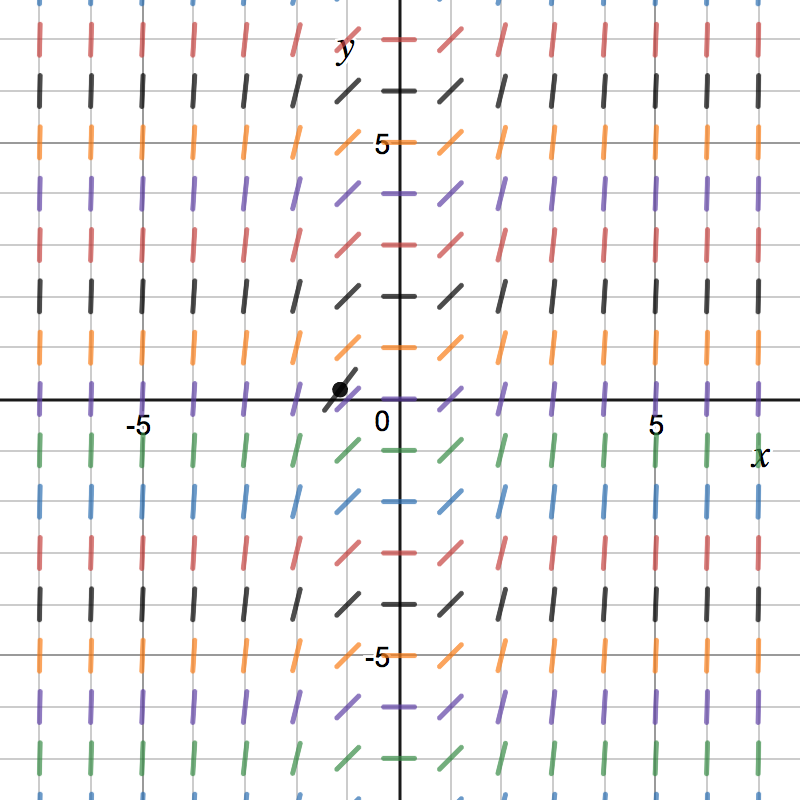
Direction Fields

Which of the following represents the direction field for $\displaystyle \frac {dy}{dx} = x^2$ ?

Which of the following represents the direction field for $\displaystyle \frac {dy}{dx} = x-y$ ?

Which of the following represents the direction field for $\displaystyle \frac {dy}{dx} = x^2-y$ ?

Which of the following represents the direction field for $\displaystyle \frac {dy}{dx} = x+y$ ?

Euler’s Method

Remember, Euler’s method is useful when trying to approximate a solution to an initial-value problem. It proceeds in steps, using the differential equation to get slopes of tangent lines, building the tangent lines, and using the line to get the next approximate value of the function. The procedure:

Suppose $\displaystyle \frac {dy}{dx} = F(x,y)$ and $y(x_0) = y_0$ (so $(x_0,y_0)$ is a point on the curve). If the step size is $h$ , then we will use the following formulas: $x_{n+1} = x_n + h,\quad y_{n+1} = y_n + F(x_n,y_n)h.$

If $\displaystyle \frac {dy}{dx} = x+y$ and $y(0) = 1$ , use a step size of $h = .5$ to approximate $y(1)$ .

We are using steps of size $.5$ to get from $x=0$ to $x=1$ , so we will need two iterations of Euler’s method. We know $(0,1)$ is on the solution curve from the given information. Our next step will be approximating the $y$ -value at $x = 0+.5 = .5$ , i.e. the point $(.5,?)$ . To get it, notice that the slope at $(0,1)$ is: $\frac {dy}{dx}\Big |_{x=0,y=1} = \answer {1}.$ So the tangent line at $(0,1)$ has slope $1$ . In theory, this would mean that our tangent line is $y = x+1$ (since the slope is $1$ and it goes through $(0,1)$ ), and so the $y$ -value at $x=.5$ is approximately $\answer {1.5}$ . Notice that this agrees with the formula: $y_1 = y_0 + F(0,1)h = 1+1(.5) = \answer {1.5},$ which is why the formula works. Therefore, the first step of Euler’s method gives an approximation of $(.5,1.5)$ .

For the second iteration, we will use this new point as our starting point. Notice $\frac {dy}{dx}\Big |_{x=.5,y=1.5} = \answer {2}.$ Therefore, at $x=1$ , we expect a $y$ -value of $y_2 = y_1 + 2h = 1.5 + 2 \cdot .5 = \answer {2.5}.$ Therefore, $y(1) \approx 2.5$ .

The solution to the above differential equation is $y = 2e^x-x-1$ . If we plug in $x=1$ , we get $2e-2 \approx 3.43$ . So this approximation was good but not great. If we used a smaller step size, we would get a better approximation.

Repeat the previous problem with a step size of $h=.2$ instead of $.5$ to approximate $y(1)$ . You may use a calculator to help you get the values. Fill out the following table, rounding all answers to four decimal places: $\begin {array}{c|c|c} n & x_n & y_n \\ \hline 0 & 0 & 1 \\ 1 & .2 & \answer {1.2} \\ 2 & .4 & \answer {1.48} \\ 3 & .6 & \answer {1.856} \\ 4 & \answer {.8} & \answer {2.3472} \\ 5 & \answer {1} & \answer {2.9766} \\ \end {array}$ Notice we get a slightly better approximation. As we decrease the step size further, we will get better approximations.

A car travels in a straight line. At time $t=0$ , the car’s position ( $s$ ) is $s(0) = 0$ . Its velocity is given by $s'(t) = t^2-s+1$ . Using Euler’s method with a step size of $1$ , we can approximate the car’s position at $t=3$ is: $s(3) \approx \answer {5}.$