Recap Video
Take a look at the following video which recaps the ideas from the section.
_
Example Video
Below are videos showing two worked examples.
Problems
Let be a continuous function on an interval .
- Part 1: If . Then is continuous on , differentiable on , and .
- Part 2: If is any antiderivative of , then .
Consider a function whose graph is shown below. 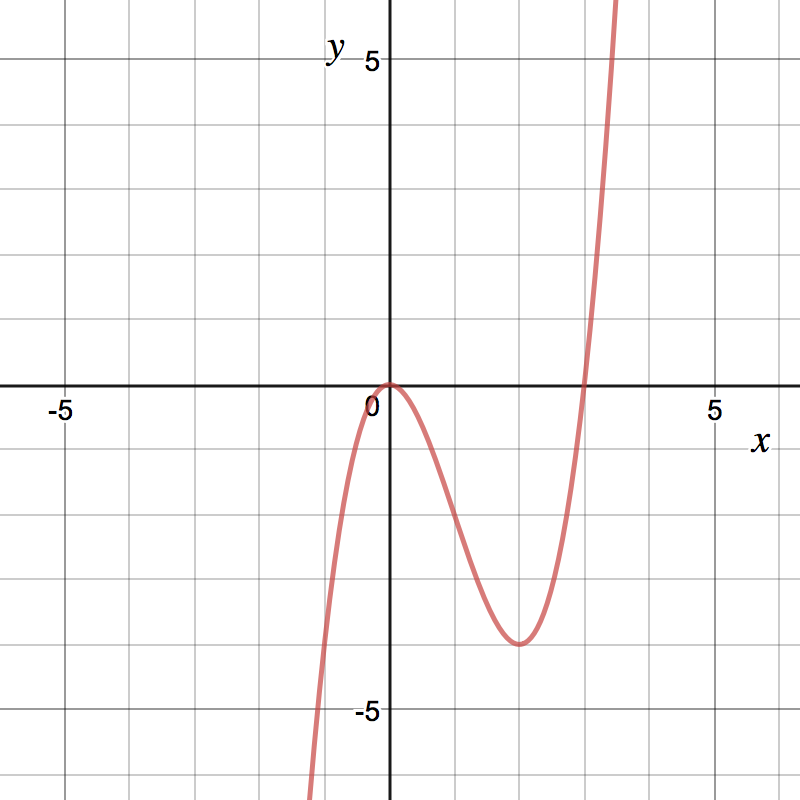 Let for .
Let for .

- What are the critical numbers of ? List them in increasing order:
- On what interval(s) is increasing? only only and only only.
- On what interval(s) is decreasing? only and and only only.
- There is a local minimum of at .
- On what interval(s) is concave up? only only and only only.
- On what interval(s) is concave down? only only and only only.
- There are inflection points of at (in increasing order) and .