Throughout this module, if something does not exist, write DNE in the
answer box.
Recap Video
Take a look at the following video which recaps the ideas from the section.
_
Example Video
Below is a video showing a worked example.
Problems
Procedure 1. Given a differentiable function and an initial guess , the
formula to get from one approximation of a root of to another is given
by
assuming .
(For this problem, you can use a calculator) Consider , whose graph is shown
below.
If an initial guess for the root is , find .
The formula for Newton’s method
is
Note that
Therefore, the formula becomes
Plugging in and using our initial value of gives (round your answer to five
decimal places).
(For this problem, you can use a calculator) Use to approximate
to decimal places.
Note that is a root of . Let’s make an initial
guess of , since this is close to . The formula for Newton’s method
is
Note that , so the formula becomes
We get the following table giving values of (round your answers to five
decimal places):
Using this, we can say that to three decimal places is .
In the previous problem, we saw that for and , we had . Which of the
following describes how is obtained?
We note that the tangent line to at
goes through the point . We see where the tangent line to at intersects the
-axis.
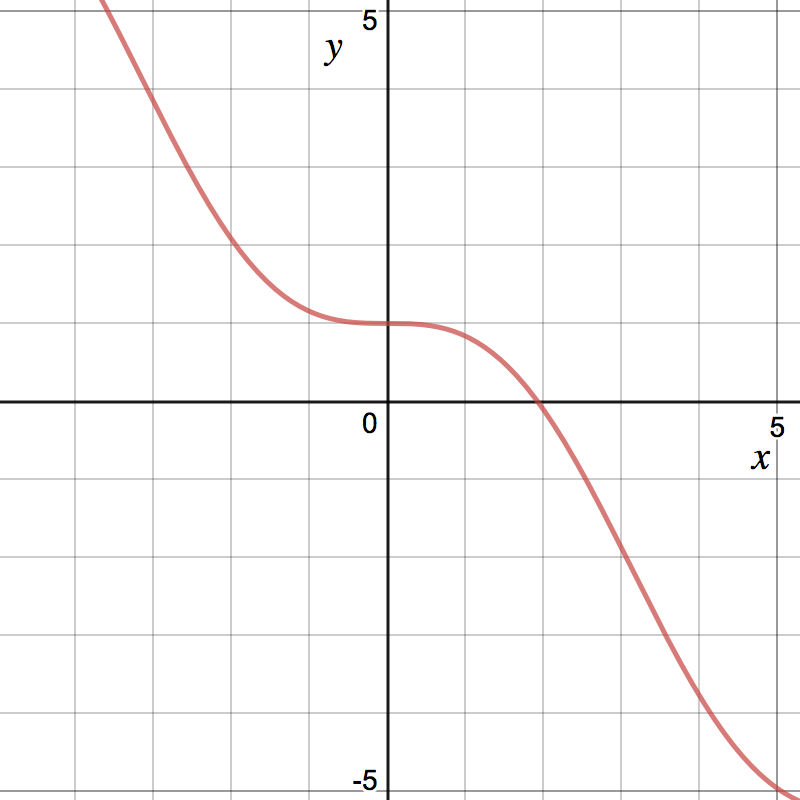 If an initial guess for the root is , find .
If an initial guess for the root is , find .
