4.7: Optimization

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

The sum of two numbers $x$ and $y$ with $x,y \geq 0$ is equal to $8$ . Find the numbers which give a maximal product.

Steps:

Step 1: Draw a picture (if applicable). In this case, we do not really need a picture.
Step 2: Assign variables and write down what needs to be maximized or minimized. In this case, we have our variables $x$ and $y$ . We want to maximize the product, so $P = xy.$
Step 3: Get the function in terms of one variable. In this case, we have two variables, and we want to bring it down to one. However, we have a relationship between $x$ and $y$ , namely that $x+y = \answer {8}$ . Therefore, we can say $y = \answer {8-x}$ . Plugging this into the product function gives $P(x) = \answer {x(8-x)}.$
Step 4: Decide on an interval (if possible). In this case, we know $x \geq 0$ from the problem. To see the largest possible $x$ -value, note that $y \geq 0$ , which means $8-x \geq 0$ . Therefore, $x \leq \answer {8}$ . This gives an interval of $[0,\answer {8}]$ .
Step 5: Find the maximum or minimum of the function on the interval. Now, we differentiate. We have $P'(x) = \answer {8-2x}.$ We find critical points. In this case, there is only one, at $x = \answer {4}$ . Since our interval is closed, we can just plug in this point and the endpoints into the function $P(x)$ . Doing so gives $P(0) = \answer {0},\quad P(4) = \answer {16},\quad P(8) = \answer {0}.$ Therefore, the maximum product is $16$ , and it happens when $x = \answer {4}$ and $y = 8-x = \answer {4}$ .

You have $100$ feet of fencing to build a rectangular pen with three parallel partitions. Find the dimensions of the pen which will maximize the area.

Steps:

Step 1: Draw a picture (if applicable). In this case, a picture will be nice:
Step 2: Assign variables and write down what needs to be maximized or minimized. Let’s have $x$ be the length of the base and $y$ the vertical height. In this case, we want the maximal area, and the area of the rectangle is $A = \answer {xy}.$
Step 3: Get the function in terms of one variable. In this case, we have two variables, and we want to bring it down to one. However, we have a constraint. Namely, we have $100$ feet of fencing. In this case, this is the perimeter plus the three partitions. Therefore, in terms of $x$ and $y$ : $\answer {2x+5y} = 100.$ Solving for $y$ in terms of $x$ , say, gives $y = \answer {20-\frac {2}{5}x}.$ Plugging this into the area function gives $A(x) = \answer {x\left (20-\frac {2}{5}x\right )}.$
Step 4: Decide on an interval (if possible). In this case, we know $x \geq 0$ from the problem (it is a length). To see the largest possible $x$ -value, note that $y \geq 0$ , which means $20-\frac {2}{5}x \geq 0$ . Therefore, $x \leq \answer {50}$ . This gives an interval of $[0,\answer {50}]$ .
Step 5: Find the maximum or minimum of the function on the interval. Now, we differentiate. We have $A'(x) = \answer {20-\frac {4}{5}x}.$ We find critical points. In this case, there is only one, at $x = \answer {25}$ . Since our interval is closed, we can just plug in this point and the endpoints into the function $A(x)$ . Doing so gives $A(0) = \answer {0},\quad A(25) = \answer {250},\quad A(50) = \answer {0}.$ Therefore, the maximum area is $250$ , and it happens when $x = \answer {25}$ feet and $y = 20-\frac {2}{5}x = \answer {10}$ feet.

Suppose we have a closed cylindrical can whose volume is $20\pi$ in $^3$ . The material for the top and bottom of the can costs $\$10/\text {in}^2$ , and the material for the side of the can costs $\$8/\text {in}^2$ . Find the dimensions which minimize the cost of the can.

Steps:

Step 1: Draw a picture (if applicable). In this case, a picture will be nice:
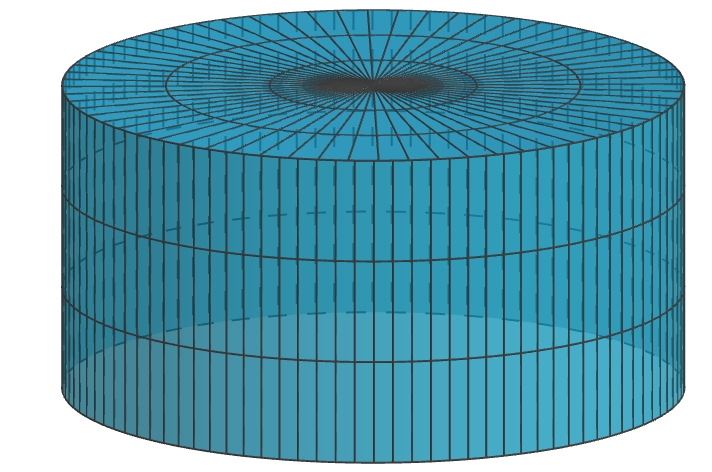
Step 2: Assign variables and write down what needs to be maximized or minimized. Let’s have $r$ be the radius of the can and $h$ be the height. We need a cost function. Notice that the surface area of the top and bottom of the can combined is $\answer {2\pi r^2}$ , and the surface area of the side of the can is $\answer {2\pi rh}$ . Therefore, the cost function will be $C = \answer {20\pi r^2+16\pi r h}.$
Step 3: Get the function in terms of one variable. In this case, we have two variables, and we want to bring it down to one. However, we have a constraint. Namely, the volume is $20\pi$ . The volume of a cylinder is $V = \answer {\pi r^2 h}$ , and setting this to $20\pi$ and solving for $h$ gives $h = \frac {20}{r^2}.$ Plugging this into the coasr function gives $C(r) = \answer {20\pi r^2+\frac {320\pi }{r}}.$
Step 4: Decide on an interval (if possible). In this case, we know $r > 0$ from the problem (it is a length). However, $r$ cannot equal zero because that makes the cost function undefined (or because you can’t have volume 100 if the radius is $0$ . To see the largest possible $r$ -value, note that $h>0$ , which means $\frac {20}{r^2} \geq 0$ . But this doesn’t give any new information, since this quantity is always positive. Therefore, our interval is $(0,\infty )$ .
Step 5: Find the maximum or minimum of the function on the interval. Now, we differentiate. We have We find critical points. This is undefined when , but this isn’t in the interval, so we don’t care. Our other critical point happens when . However, the interval isn’t closed, so we have to justify our answer some other way. There are two ways:
- Approach 1: Use the first derivative test. On the interval $(0,2)$ , the derivative $C'(r)$ is , and on the interval $(2,\infty )$ , the derivative $C'(r)$ is . So on $(0,2)$ , the function $C(r)$ is , and on $(2,\infty )$ , the function $C(r)$ is , which makes $r = 2$ a local maximumminimum . Since it is the only critical point, it must be the global minimum.
- Approach 2: Use the second derivative test. Notice $C''(r) = \answer {40\pi + \frac {640\pi }{r^3}}.$ Plugging in $r=2$ gives $C''(2) = \answer {120\pi } > 0$ , so $r=2$ is a local maximumminimum . Since it is the only critical point, it must be the global minimum.
Either way, we get a global min when $r= 2$ inches and $h = \answer {5}$ inches.

The point on $y = \sqrt {x}$ closest to the point $(4,0)$ is $(\answer {7/2},\answer {\sqrt {7/2}})$ .