4.5: Curve Sketching

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

Sketch the graph of $f(x) = x^4+4x$ .

We will break this into steps:

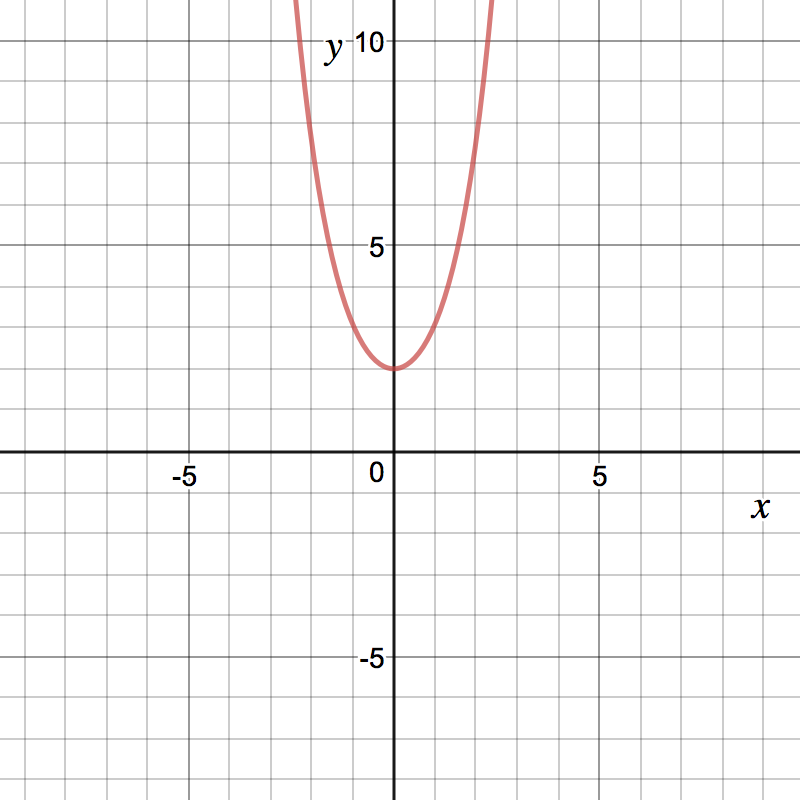
Asymptotes and intercepts: Does the graph of $f(x)$ have any horizontal asymptotes?
Yes No
Does the graph of $f(x)$ have any vertical asymptotes?
Yes No
The $x$ -intercepts of $f(x)$ , in increasing order, are at $x = \answer {-4^{1/3}},\quad x = \answer {0}.$ The $y$ -intercept of $f(x)$ is at $y = \answer {0}$ .
Increasing/Decreasing and Extrema: We find critical points of . Notice This is defined everywhere, and when . So this is our lone critical point. Using our first derivative test, we can find:
- On $(-\infty ,-1)$ , the function $f(x)$ is increasingdecreasing .
- On $(-1,\infty )$ , the function is increasingdecreasing .
This also tells us that there is a local at $x=-1$ . The coordinate on the graph of $f(x)$ is $(-1,\answer {-3})$ .
Concavity and Inflection Points: Notice This is defined everywhere, and is equal to when . Using our number line, we get that:
- On $(-\infty ,0)$ , the function $f(x)$ is concave updown .
- On $(0,\infty )$ , the function is concave updown .
Is there an inflection point at $x=0$ ?
Yes No

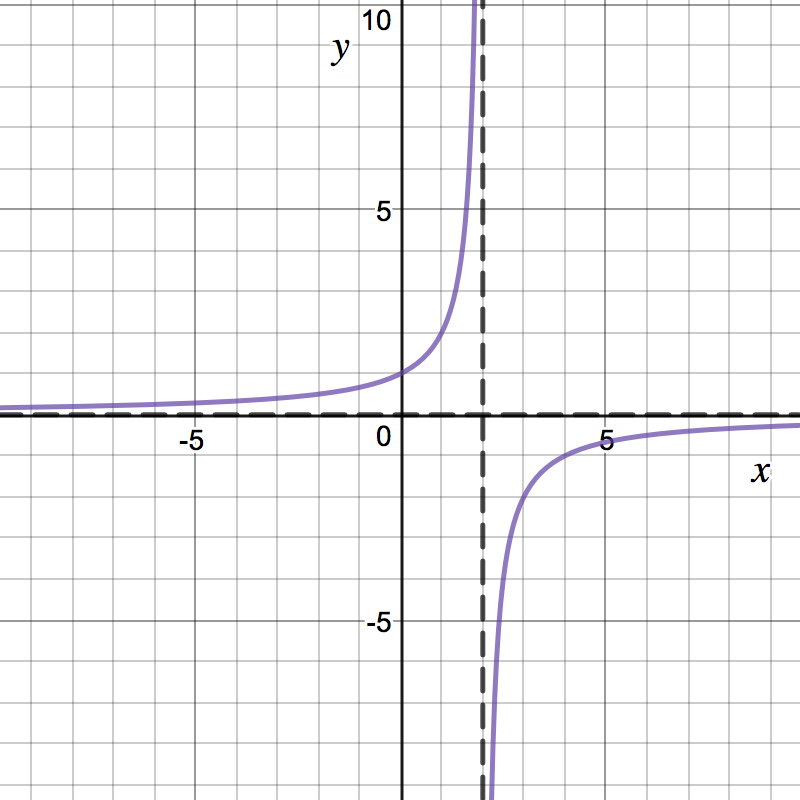
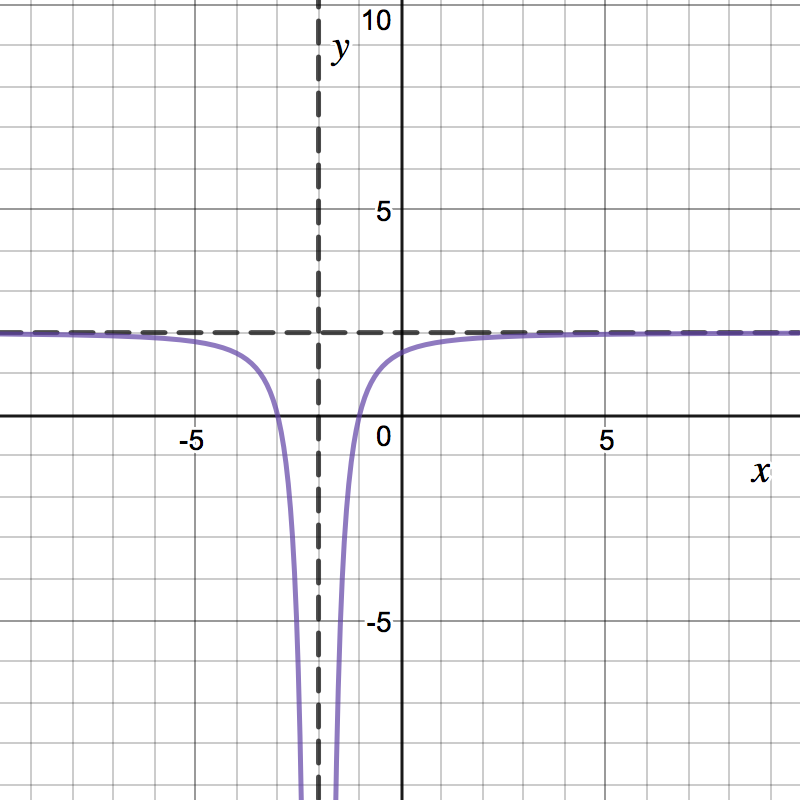
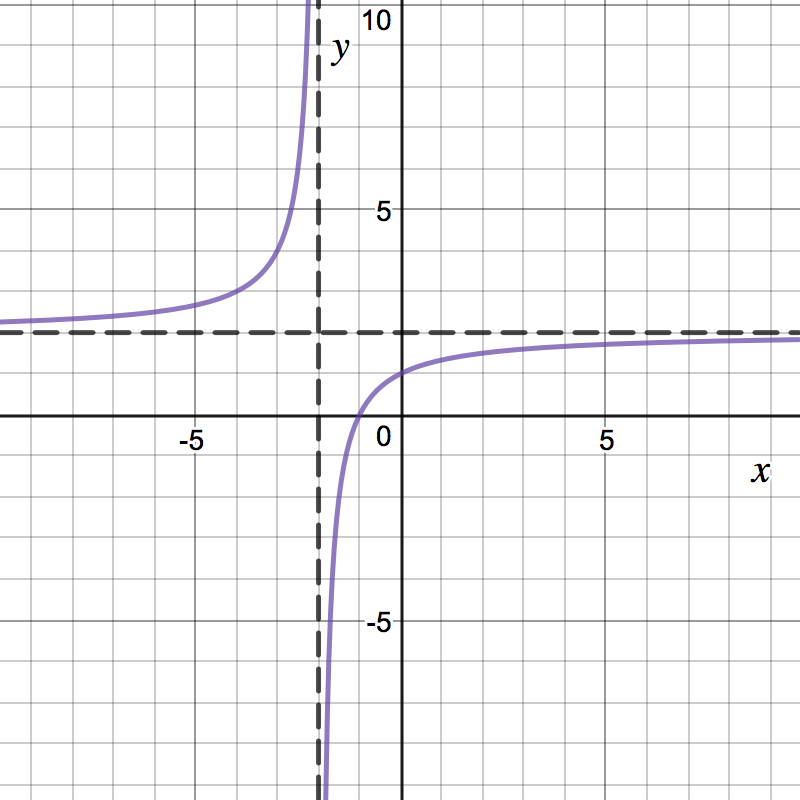
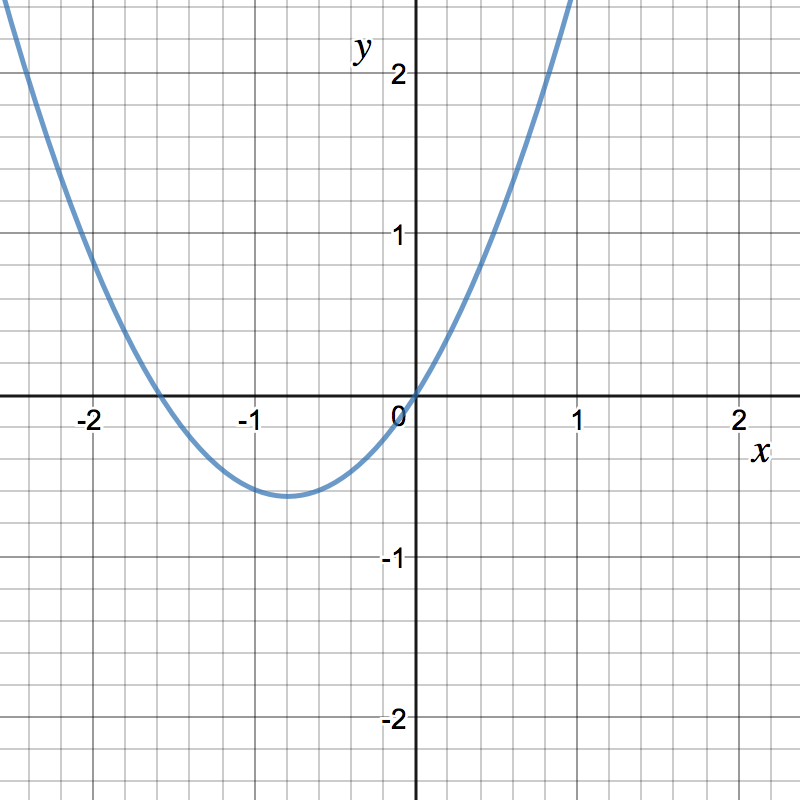
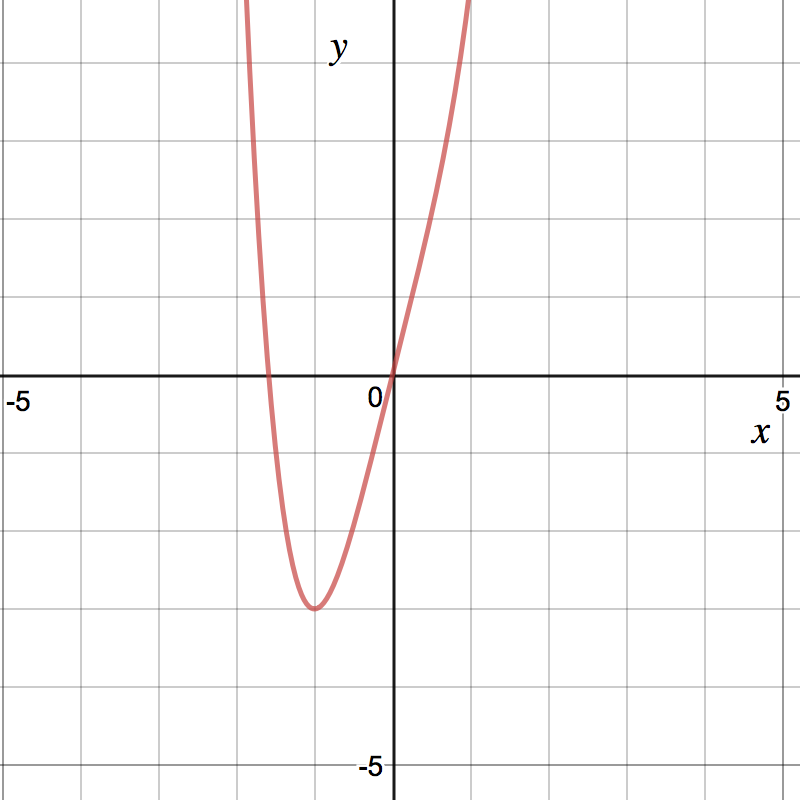
Now, we can put all this information together. Try sketching the graph on your own first. Which of the following is the graph of $f(x)$ ?

Sketch the graph of $\displaystyle f(x) = 1+ \frac {x}{x+2}$ .

We will break this into steps:

Asymptotes and intercepts: The graph has a horizontal asymptote at $y = \answer {2}$ and a vertical asymptote at $x = \answer {-2}$ . The $x$ -intercept of $f(x)$ is at $(\answer {-1},0)$ , and the $y$ -intercept of $f(x)$ is $(0,\answer {1})$ .
Increasing/Decreasing and Extrema: We find critical points of . Notice This is undefined at (this is not, technically, a critical point since this point was not in the domain of , but we still need to consider it). We also get when (if no suchpoint exists, write DNE). Using our first derivative test, we can find:
- On $(-\infty ,-2)$ , the function $f(x)$ is increasingdecreasing .
- On $(-2,\infty )$ , the function is increasingdecreasing .
Concavity and Inflection Points: Notice This is undefined at . We also get when (if no suchpoint exists, write DNE).
- On $(-\infty ,-2)$ , the function $f(x)$ is concave updown .
- On $(-2,\infty )$ , the function is concave updown .
Is there an inflection point at $x=-2$ ?
Yes No

Now, we can put all this information together. Try sketching the graph on your own first. Which of the following is the graph of $f(x)$ ?

Sketch the graph of $f(x) = e^x+e^{-x}$ . Label all asymptotes, local extrema, and inflection points. Which of the following is the graph of $f(x)$ ?