4.2: Mean Value Theorem

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

We have two new theorems:

Mean Value Theorem Suppose $f(x)$ is continuous on $[a,b]$ and differentiable on $(a,b)$ . Then there is a point $c$ in $(a,b)$ with $f'(c) = \frac {f(b)-f(a)}{b-a}.$

Rolle’s Thoerem Suppose $f(x)$ is continuous on $[a,b]$ and differentiable on $(a,b)$ , and that $f(b)=f(a)$ . Then there is a point $c$ in $(a,b)$ with $f'(c) = 0$ .

Notice Rolle’s Theorem follows from the Mean Value Theorem (MVT) by taking $f(b)=f(a)$ in the MVT.

Consider $f(x) = x^2$ on the interval $[0,2]$ .

What is the slope of the secant line between $(0,f(0))$ and $(2,f(2))$ ?
This is something we’ve encountered before. We have the points $(0,\answer {0})$ and $(2,\answer {4})$ , and the slope of the line between them is $\answer {2}$ .
Here is the graph of $y=f(x)$ .

By inspecting the graph, at what point in $(0,4)$ does it seem like the slope of the tangent line is the same as the slope of the secant line found above?
We want the slope to be $2$ . It looks like the tangent line has slope $2$ at $x = \answer {1}$ .
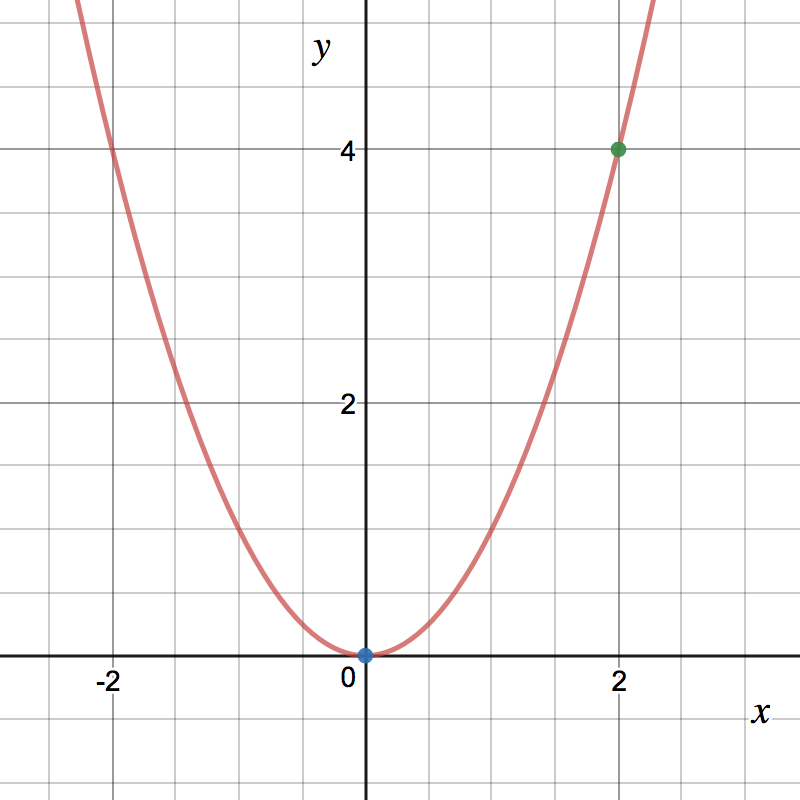
Find the $c$ such that the tangent line to the graph at $x=c$ matches the slope of the secant line between $(0,0)$ and $(2,4)$ .
The slope of the tangent line is $f'(c)$ . Notice $f'(x) = \answer {2x}$ , so $f'(c) = \answer {2c}$ . We want this to be $2$ , so we set $2c=2$ , which means $c = \answer {1}$ , confirming our answer from the previous part.

Consider $f(x) = \sqrt {x}$ on the interval $[0,16]$ .

Do the hypotheses of the MVT apply?
Yes No
The $x$ -value $x=c$ satisfying the conclusion of the MVT is $c = \answer {4}$ .
Which of the following illustrates the MVT and your answer to the previous part?

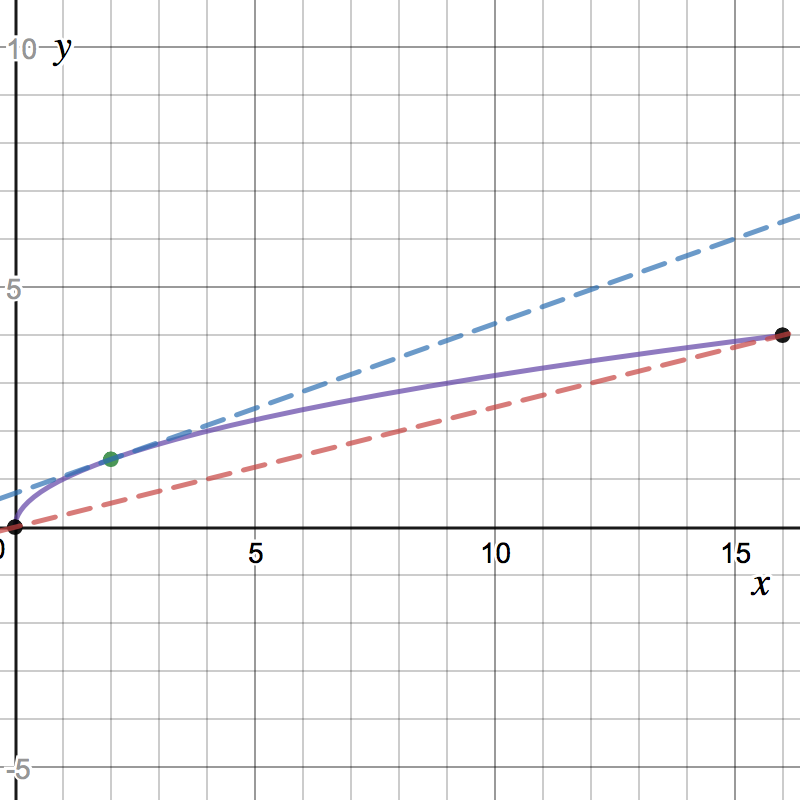
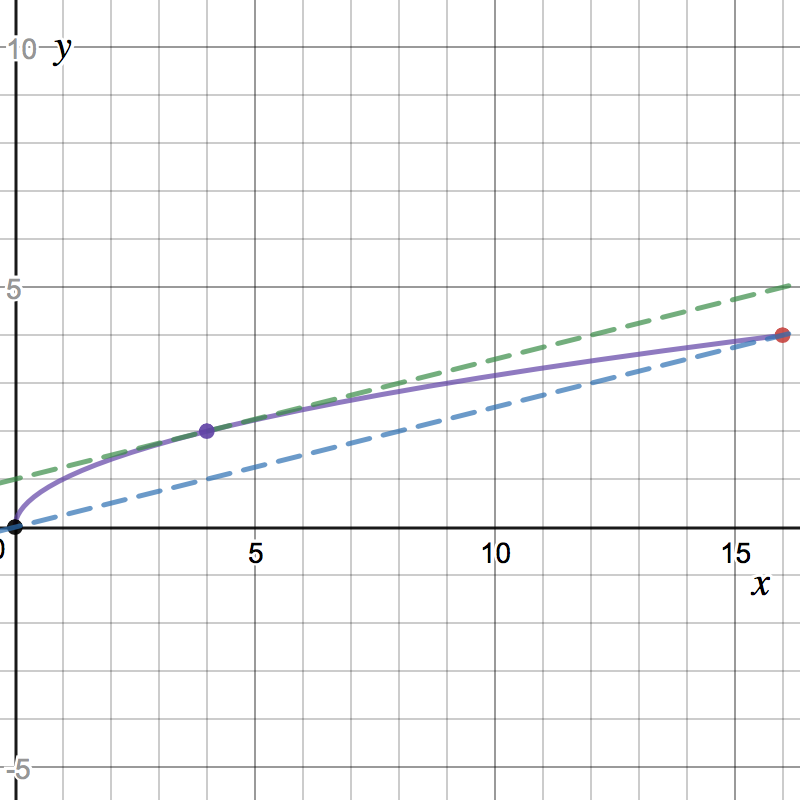
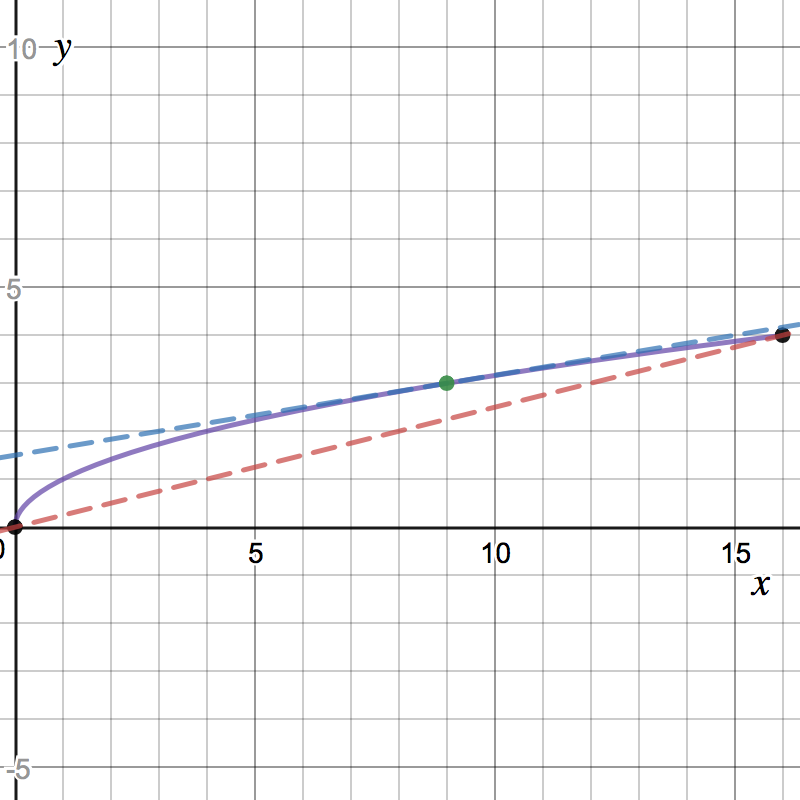
Consider $f(x) = x^{2/3}$ on the interval $[-1,1]$ . Do the hypothesis of the MVT apply?

Yes No

Why not?

The function is not continuous on $[-1,1]$ . The function is not differentiable on $(-1,1)$ .

Now we will see what can go wrong if the hypotheses aren’t satisfied. What is the slope of the secant line of $f(x)$ between $(-1,f(-1))$ and $(1,f(1))$ ? $\answer {0}$ .

What is the derivative of $f(x)$ ? $f'(x) = \answer {\frac {2}{3}x^{-1/3}}$ .

Is there any point where $f'(x)= 0$ ? YesNo . This means the conclusion of the MVT isn’t necessarily satisfied if the hypotheses are not satisfied.

Suppose $f(x)$ is a differentiable function with $f(1)=2$ and $f'(x) \leq 3$ for all $x$ . What is the largest possible value of $f(3)$ ? $\answer {8}$ .

Which of the following are consequences of Rolle’s Theorem for an everywhere differentiable function $f(x)$ ? Select all that apply.

If $f(a) = f(b)$ , then between $x=a$ and $x=b$ there must be a horizontal tangent line. Between any two roots of $f(x)$ , there is a root of $f'(x)$ . Between any two roots of $f(x)$ , there is a point where $f'(x)$ has a horizontal tangent line. If $f'(x)>0$ , then $f(x)$ has at most one root.

Show that $f(x) = x^3+x+1$ has at most one real root.

From the previous problem, we know that Rolle’s Theorem tells us that between any two roots of $f(x)$ there is a root of $f'(x)$ (i.e. a horizontal tangent line to the graph of $f(x)$ ). This means the number of roots of $f(x)$ is at most one more than the number of roots of $f'(x)$ (make sure you think through this). Notice $f'(x) = \answer {3x^2+1}.$ Are there any points where $f'(x) = 0$ ?

Yes No

This tells us $f'(x)$ has no roots (in fact, $f'(x)>0$ for all $x$ ). Therefore, Rolle’s Theorem tells us that $f(x)$ has at most one root (if it had two, there would need to be a root of $f'(x)$ between them, but there is no such root of $f'(x)$ ).

Notice that we could use the Intermediate Value Theorem to show that $f(x)$ has at least one root, so this would show that $f(x)$ has exactly one root.

Using the strategy outlined in the previous problem, Rolle’s Theorem tells us that $f(x) = x^4+x^3+x^2$ at most how many roots? $\answer {2}$ .