3.9: Related Rates

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

The side of a cube is increasing at a rate of $2$ inches/second. How fast is the volume changing at the moment the side length is $3$ inches.

Let’s draw a picture.

Let’s call the length of one side $s$ . To say that the side of the cube is increasing at a rate of $2$ inches/second means that $\frac {ds}{dt} = \answer {2}.$ Note that $ds/dt > 0$ since $s$ is increasing. We are looking for the rate of change of the volume. If the volume is $V$ , this means we are looking for $\displaystyle \frac {dV}{dt}$ . We know the relationship between $V$ and $s$ for a cube, namely $V = \answer {s^3}.$ Since $V$ and $s$ are functions of $t$ , this could be written more suggestively as $V(t) = [s(t)]^3$ . We can differentiate both sides with respect to $t$ , noting that we have to use chain rule on the right side. Doing this gives $\frac {dV}{dt} = \answer {3s^2}\frac {ds}{dt}.$ We know $ds/dt = 2$ , and the question is asking for the rate of change of the volume when $s = \answer {3}$ . Plugging these in gives $\frac {dV}{dt}\Big |_{s=3} = \answer {54}.$ The units are inches/secondinches $^2$ /secondinches $^3$ inches $^3$ /second .

In the same situation as the previous problem, at what rate is the surface area of the cube changing at the moment the side length is $3$ inches? $\answer {72}$ inches/secondinches $^2$ /secondinches $^3$ inches $^3$ /second .

You are standing 7 miles away from a rocket launchpad and are watching with a telescope. A rocket takes off and rises you watch the rocket through your telescope. At a certain moment, the rocket is rising at a rate of 5 miles/min and the angle between the telescope and the ground is $\pi /3$ . At what rate is the angle between the telescope and the ground changing at this moment?

Here is a picture to model the situation, taken from Rogawski’s “Calculus”: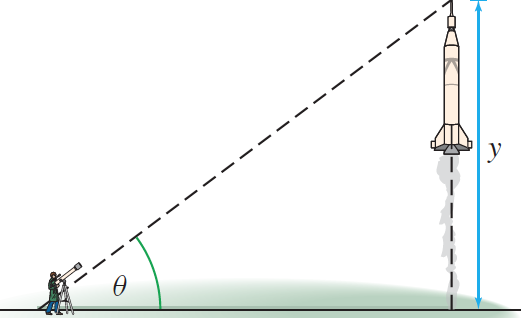

If the rocket’s height is $y$ , then the rocket’s velocity is $\frac {dy}{dt} = \answer {5}.$ We know the distance between the telescope and the launchpad is $7$ miles. Which trig function relates this side, $\theta$ , and $y$ ?

sine cosine tangent

Therefore, we can say $\tan (\theta ) = \answer {y/7}$ . The question is asking for $d\theta /dt$ . Differentiating both sides of the above relation with respect to $t$ gives $\answer {\sec ^2(\theta )}\frac {d\theta }{dt} = \answer {\frac {1}{7}}\frac {dy}{dt}.$ We know $dy/dt$ . We are looking for $d\theta /dt$ at the moment $\theta = \answer {\pi /3}$ . We know $\sec ^2(\pi /3) = \answer {4}.$ Plugging this into the above relation gives $4\frac {d\theta }{dt} = \frac {1}{7} \cdot 5.$ Therefore, $\frac {d\theta }{dt} = \answer {\frac {5}{28}} \text {radians/min.}$

In the above problem, at what rate is the distance between the rocket and the telescope changing at the moment the rocket’s velocity is $5$ miles/min and the angle between the telescope and the ground is $\pi /3$ ? $\answer {\frac {35\sqrt {3}}{14}}$ miles/min.

A particle moves around the circle $x^2+y^2=2$ counterclockwise.

In which quadrants is $dx/dt > 0$ ? Select all that apply.
Quadrant 1 Quadrant 2 Quadrant 3 Quadrant 4
If the particle’s $x$ -coordinate is decreasing at a rate of $2$ units/second at the point $(1,1)$ on the circle, at what rate is the particle’s $y$ -coordinate changing at this moment? It is at a rate of $\answer {2}$ units/second.

A conical tank has a height of $3$ feet and a radius of $2$ feet on the top. Water is flowing in at $2$ cubic feet/minute. At what rate is the water level rising when the level is $2$ feet? $\answer {\frac {9}{8\pi }}$ feet/minute.

Suppose the volume of a sphere is decreasing at $32 \pi$ cubic feet/min. At what rate is its surface area changing at the moment the radius is $2$ feet? $\answer {-32\pi }$ feet $^2$ /min.