3.5: Implicit Differentiation

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

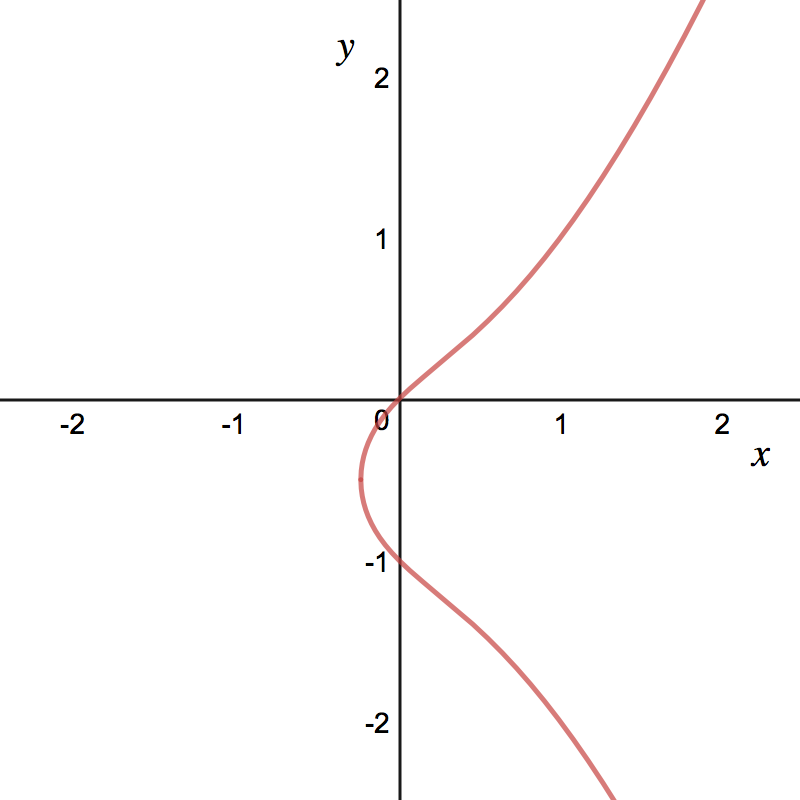
Idea: Remember, the idea of implicit differentiation is the following. We will have some relation with $x$ ’s and $y$ ’s, such as the following: $y^2+y = x^3+x.$ As we see in the following graph, this is not the graph of a function.

However, we still want to look for slopes of tangent lines. What we do is say, near a point, that this relation gives $y$ in terms of $x$ (zoom in far enough so that it looks like a function). In this case, you can solve for $y$ , though it won’t look too nice. So we want to get around this. This is what implicit differentiation is used for.

If $y^2+y = x^3+x$ , find $\displaystyle \frac {dy}{dx}$ at the point $(1,1)$ .

We will assume that, near the point $(1,1)$ , that $y$ is a function of $x$ . We will write $y(x)$ or $y = f(x)$ to help us remember this. So the relation above says $y(x)^2 + y(x) = x^3+x.$ We will now take the derivative of both sides: $\frac {d}{dx}[y(x)^2+y(x)] =\frac {d}{dx}[x^3+x].$ On the left side, we will need to use the chain rule. Notice that $y(x)$ is a composition as follows: $x \stackrel {f(x)}{\longrightarrow } y \stackrel {x^2}{\longrightarrow } y^2.$ So the derivative of $y(x)^2$ is $2y(x)\cdot y'(x)$ , or $2y\cdot y'$ for short. Similarly, the derivative of $y(x)$ is $y'$ . We can differentiate the right side normally. Therefore, we have $2yy' + y' = \answer {3x^2+1}.$ Solving for $y'$ gives $y' = \frac {\answer {3x^2+1}}{\answer {2y+1}}.$ Plugging in $(1,1)$ gives $\frac {dy}{dx}\Big |_{(1,1)} = \answer {\frac {4}{3}}.$

Find the equation of the tangent line to $y^2+y=x^3+x$ at the point $(1,1)$ .

We have the slope from the previous problem, and we have the point $(1,1)$ . Therefore, the line is $y = \answer {\frac {4}{3}x-\frac {1}{3}}.$

If $x^2+xy+y^2=3$ , find $y'$ .

We repeat the process of the first implicit problem above. We can read this as, for example, $x^2+xf(x)+f(x)^2=3.$ Now we see that if we were to differentiate this with respect to $x$ , the second term would require power ruleproduct rulequotient rule . Differentiating both sides with respect to $x$ gives $2x+xy'+y+2yy' = \answer {0}.$ (Notice the use of product rule in the second term and chain rule in the third term.) Solving for $y'$ gives $y' = \answer {-\frac {2x+y}{x+2y}}.$

Find all points on $x^2+xy+y^2=3$ where the tangent line is horizontal.

In the previous problem, we found $y' = -\frac {2x+y}{x+2y}.$ To see where the tangent line is horizontal, we need to set $y' = \answer {0}$ . This will happen when $-\frac {2x+y}{x+2y} = 0.$ A fraction is zero if the numerator is zero, so we can say $y' = 0$ when $y = \answer {-2x}$ . To get the actual points, we can plug this into the original relation: $x^2+x(-2x)+(-2x)^2 = 3,$ or $3x^2=3$ . Solving gives, in increasing order, $x = \answer {-1} \quad \text { and } \quad x = \answer {1}.$ Since $y=-2x$ , we get two points: $(-1,\answer {2}),\quad (1,\answer {-2}).$

If $(x-y)^2 = x+y-1$ , then the equation of the tangent line to $(1/2,1/2)$ is $y=\answer {-x+1}.$

Using the ideas of implicit differentiation, we can find the following derivatives:

$\displaystyle \frac {d}{dx}\sin ^{-1}(x) = \frac {1}{\sqrt {1-x^2}}$ .
$\displaystyle \frac {d}{dx}\cos ^{-1}(x) = \frac {-1}{\sqrt {1-x^2}}$ .
$\displaystyle \frac {d}{dx}\tan ^{-1}(x) = \frac {1}{1+x^2}$ .

The equation of the tangent line to $y = \sin ^{-1}(2x)$ at the point $x=\sqrt {3}/4$ is: $y = \answer {4x-\sqrt {3}+\frac {\pi }{3}}.$