2.5: Continuity and IVT

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Throughout this module, if something does not exist, write DNE in the answer box.

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below are two videos showing worked examples.

Example 1:

Example 2:

Problems

A function $f(x)$ is continuous at $x=a$ if:

$f(a)$ exists.
$\lim _{x \to a} f(x)$ exists.
$\lim _{x \to a} f(x) = f(a)$ .

We can say $f(x)$ is right-continuous (resp. left-continuous) if replace all limits above with limits from the right (resp. left).

Remember that the types of discontinuity:

Removable: $\lim _{x \to a} f(x)$ exists but is not equal to $f(a)$ .
Jump: $\lim _{x \to a^-} f(x) \neq \lim _{x \to a^+} f(x)$ (but both of these limits exist).
Infinite: $\lim _{x \to a^+}f(x)$ or $\lim _{x \to a^-} f(x)$ is $\pm \infty$ .

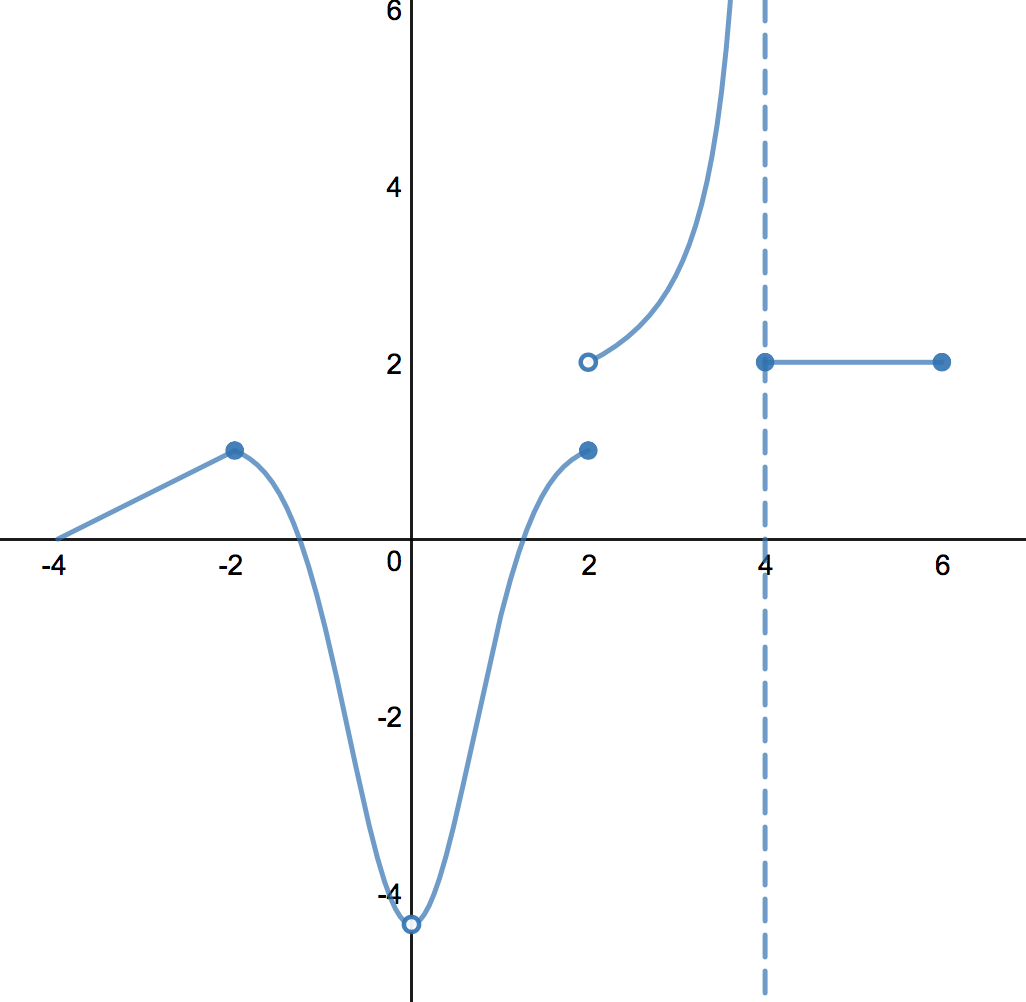
For the following graph of a function $f(x)$ , decide whether the function is continuous. If not, decide the type of discontinuity.

At $x=-2$ : $f(x)$ is continuoushas a removable discontinuityhas a jump discontinuityhas an infinite discontinuity .
At $x=0$ : $f(x)$ is continuoushas a removable discontinuityhas a jump discontinuityhas an infinite discontinuity
At $x=4$ : $f(x)$ is continuoushas a removable discontinuityhas a jump discontinuityhas an infinite discontinuity
At $x=2$ : $f(x)$ is continuoushas a removable discontinuityhas a jump discontinuityhas an infinite discontinuity

For the graph below (same graph as previous problem), decide whether the function is right-continuous, left-continuous, both, or neither.

At $x=-2$ : $f(x)$ is right-continuousis left-continuousis both left- and right- continuousis neither left- nor right- continuous
At $x=0$ : $f(x)$ is right-continuousis left-continuousis both left- and right- continuousis neither left- nor right- continuous
At $x=4$ : $f(x)$ is right-continuousis left-continuousis both left- and right- continuousis neither left- nor right- continuous
At $x=2$ : $f(x)$ is right-continuousis left-continuousis both left- and right- continuousis neither left- nor right- continuous

Consider the following function $f(x) = \begin {cases} x+3, & \text { if } x\leq 2 \\ 5-x^2, & \text { if } 2<x \leq 3 \\ ax+5, & \text { if } x > 3 \end {cases}$ Here $a$ is some constant.

Determine whether the function $f(x)$ is continuous at $x=2$ . If not, determine the type of discontinuity, and also say whether the function is left-continuous or right-continuous at $x=2$ .
We will check the three conditions in the definition of continuity. First, we check that $f(2)$ exists. In this case, we get that $f(2) = \answer {5}$ , so that condition is satisfied. Second, we check the limit. Since $f(x)$ has different definitions to the left and right of $x=2$ , we need to compute the two one-sided limits. To the left of $x=2$ , the function is equal to , and so $\lim _{x \to 2^-} f(x) = \lim _{x \to 2^-} \answer {x+3} = \answer {5}.$ To the right of $x=3$ , the function is equal to , and so $\lim _{x \to 2^+} f(x) = \lim _{x \to 2^+} \answer {5-x^2} = \answer {1}.$ Since the left limit doesn’t equal the right limit, the function continuous, and the function has a discontinuity. Since $f(2)$ is equal to the , the function is at $x=2$ .
Determine the value of $a$ that will make the function continuous at $x=3$ .
The approach is similar to that of the previous part. Notice $f(3) = \answer {-4}$ . For the limit, we will compute the right and left limits separately. A little to the left of $x=3$ , the function is equal to , so $\lim _{x \to 3^-} f(x) = \lim _{x \to 3^-} \answer {5-x^2} = \answer {-4}.$ To the right of $x=3$ , the function is equal to , so $\lim _{x \to 3^+} f(x) = \lim _{x \to 3^+} (ax+5) = \answer {3a+5}.$ For the limit to exist, we need the left and right limit to be equal, so we need $3a+5 = \answer {-4}.$ Solving for $a$ gives $a = \answer {-3}$ . Notice that this would make the limit $-4$ , and this would equal the value of the function, so this is the value of $a$ which makes the function continuous.

One of the nice things about continuity is that is gives us a quick way of evaluating limits: plug in the point.

Evaluate $\lim _{x \to 3} \frac {x^2+1}{\sin (\pi x)+4}$ .

Notice that both the numerator and denominator are continuous at all points, so their quotient will be continuous provided the denominator is nonzero. This means we can plug in $x=3$ to evaluate the limit: $\lim _{x \to 3} \frac {x^2+1}{\sin (\pi x)+4} = \answer {5/2}.$

Evaluate $\lim _{x \to 0} e^{x^2-5x}$ .

Since $f(x) = x^2-5x$ is continuous and $g(x) = e^x$ is continuous (i.e. polynomials and exponentials are continuous functions), their composition $g(f(x))$ is continuous, and that composition is exactly $e^{x^2-5x}$ . Therefore, we can plug in $x=0$ to evaluate the limit: $\lim _{x \to 0} e^{x^2-5x} = \answer {1}.$

Remember that in 2.3, we saw that if we plug in the point and get $0/0$ , then we need to do some algebra to figure out the limit, and if we get some other number divided by $0$ , then we will have a vertical asymptote of some kind. The same thing applies here.

The limit $\lim _{x \to -2} (x^2+5)\cos (x+2) = \answer {9}$ .

Plug in $x=-2$ into the function, which you can do because the function is continuous.

The limit $\lim _{x \to 0} \frac {x\sin (x)}{\sin (x)+\sin ^2(x)} = \answer {0}$ .

When you plug in $x=0$ , you get $0/0$ , so we need to do some algebra. Notice that the denominator factors as $\sin (x)+\sin ^2(x) = \sin (x)(\answer {\sin (x)+1}).$ Therefore

$\begin{eqnarray*} \lim_{x \to 0} \frac{x\sin(x)}{\sin(x)+\sin^2(x)} &=& \lim_{x \to 0} \frac{x\sin(x)}{\sin(x)[\sin(x)+1]} \\ &=& \lim_{x \to 0} \frac{x}{\answer{\sin(x)+1}} \\ &=& \answer{0}. \end{eqnarray*}$

The limit $\lim _{x \to 0} \frac {\sin ^2(x)}{1-\cos (x)} = \answer {2}$ .

Use $\sin ^2(x) = 1-\cos ^2(x) = (1-\cos (x))(1+\cos (x))$ .

The limit $\lim _{x \to 0^+} \frac {\sin (x)+1}{x^3+x} = \answer {\infty }$ .

When you plug in $x=0$ , you get $1/0$ , so we have an asymptote. To see whether the limit is $\pm \infty$ , imagine plugging in a small number a tad bigger than $0$ . Is the fraction positive or negative?

Intermediate Value Theorem

Intermediate Value Theorem Let $f(x)$ be a function which is continuous on an interval $[a,b]$ . If $N$ is any number between $f(a)$ and $f(b)$ , then there exists a number $c$ in the interval $[a,b]$ such that $f(c) = N$ .

(To think about) Why is it necessary that $f(x)$ be continuous? Can you think of what can go wrong if $f(x)$ is not continuous?

A root of a function $f(x)$ is a solution to $f(x) = 0$ . Show that there is a root of $f(x) = x^3-x+1$ on the interval $[-2,0]$ .

First, note that $f(x)$ isis not a continuous function, so the IVT can be applied. Second, observe that $f(-2) = \answer {-5},\quad f(0) = \answer {1}.$ What this means is that, on the interval $[-2,0]$ , the function $f(x)$ must hit every $y$ -value between $-5$ and $1$ . Since $-5 \leq 0 \leq 1$ , we know from the IVT there must be some value in the interval $[-2,0]$ which is a root of $f(x)$ .

Show that $\sin (x) = 1-x$ has a solution.

To help us apply the IVT, let’s move all the $x$ ’s to one side, so we will show that $\answer {\sin (x)+x} = 1$ has a solution. The previous problem provided the interval, whereas this one does not, so we will just have to be clever and pick an interval. The goal should be to create an interval such that the $y$ -value of $1$ lies between the $y$ -values of the two endpoints. Let’s start with $x=0$ . Notice that if $f(x) = \sin (x)+x$ , then $f(0) = \answer {0}.$ This is greater thanless than $1$ , so we now need to pick a different $x$ -value which has a $y$ -value greater than $1$ . Think about $x=\pi$ . We can compute $f(\pi ) = \answer {\pi },$ which is greater thanless than $1$ . Therefore, if we consider the interval $[0,\pi ]$ , we have $f(0) \leq 1 \leq f(\pi )$ , so the IVT tells us there is some solution in $[0,\pi ]$ , which is what we wanted!

Now you can try one:

Show that $2^x = 3^x-2$ has a solution.

True/False

Determine whether the following statements are true (meaning always true) or false. If false, try to think of a counterexample.

Suppose $f(x)$ is continuous at $x=2$ . Then it must be true that $f(x)$ is left-continuous at $x=2$ .

True False

Suppose $\lim _{x \to 3} f(x)$ exists. Then it must be true that $f(x)$ is continuous at $x=3$ .

True False

Suppose $f(x)$ is a function with a removable discontinuity at $x=5$ . Then it must be true that $f(5)$ does not exist.

True False

Suppose $f(x)$ is a continuous function. If $f(0) = 4$ and $f(1) = 5$ , then it must be true that $f(x) = 6$ has no solution in $[0,1]$ .

True False

Suppose $f(x)$ is a function with $f(0) = 1$ and $f(3) = 9$ . Also assume that $f(x) = N$ has a solution for every value of $N$ between $1$ and $9$ . Then it must be true that $f(x)$ is continuous on $[0,3]$ .

True False