2.2: Limits with Tables and Graphs

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Recap Video

Take a look at the following video which recaps the ideas from the section.

Example Video

Below is a video showing a worked example.

Problems

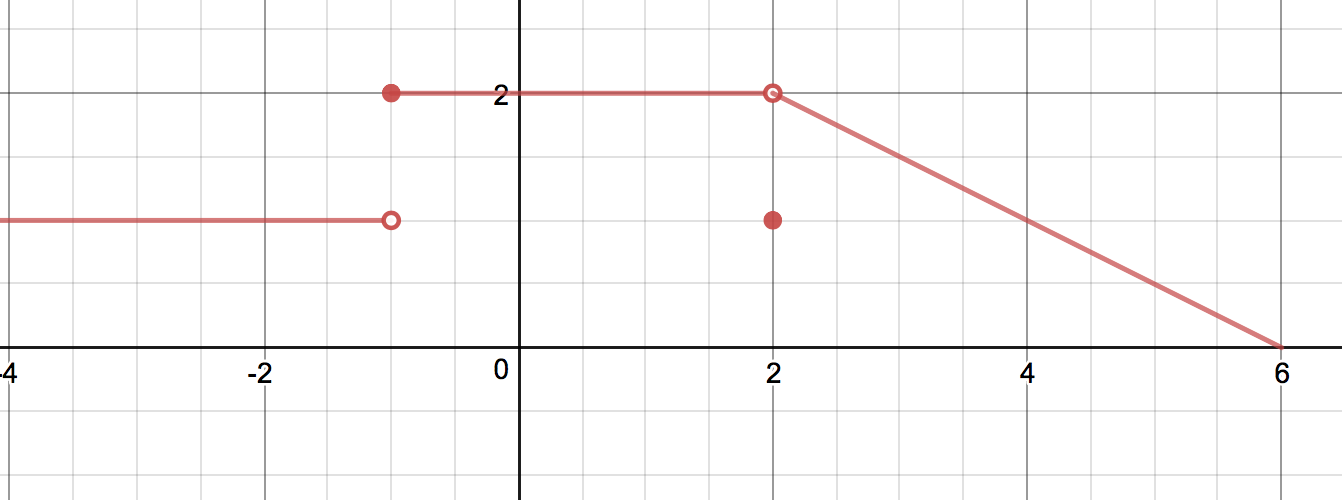
Given a function $f(x)$ :

The limit $\lim _{x \to a} f(x)$ is the value the function $f(x)$ approaches as $x$ gets closer to $a$ (if it exists).
The left-hand limit $\lim _{x \to a^-} f(x)$ is the value the function $f(x)$ approaches as $x$ gets closer to $a$ for values $x<a$ (if it exists).
The right-hand limit $\lim _{x \to a^+} f(x)$ is the value the function $f(x)$ approaches as $x$ gets closer to $a$ for values $x>a$ (if it exists).

The limit $\lim _{x \to a} f(x)$ exists if and only if $\lim _{x \to a^-} f(x) = \lim _{x \to a^+} f(x)$ .
We write a limit equals $\infty$ (resp. $-\infty$ ) if the values of $f(x)$ get arbitrarily large (resp. arbitrarily large in the negative direction) as $x$ approaches $a$ .

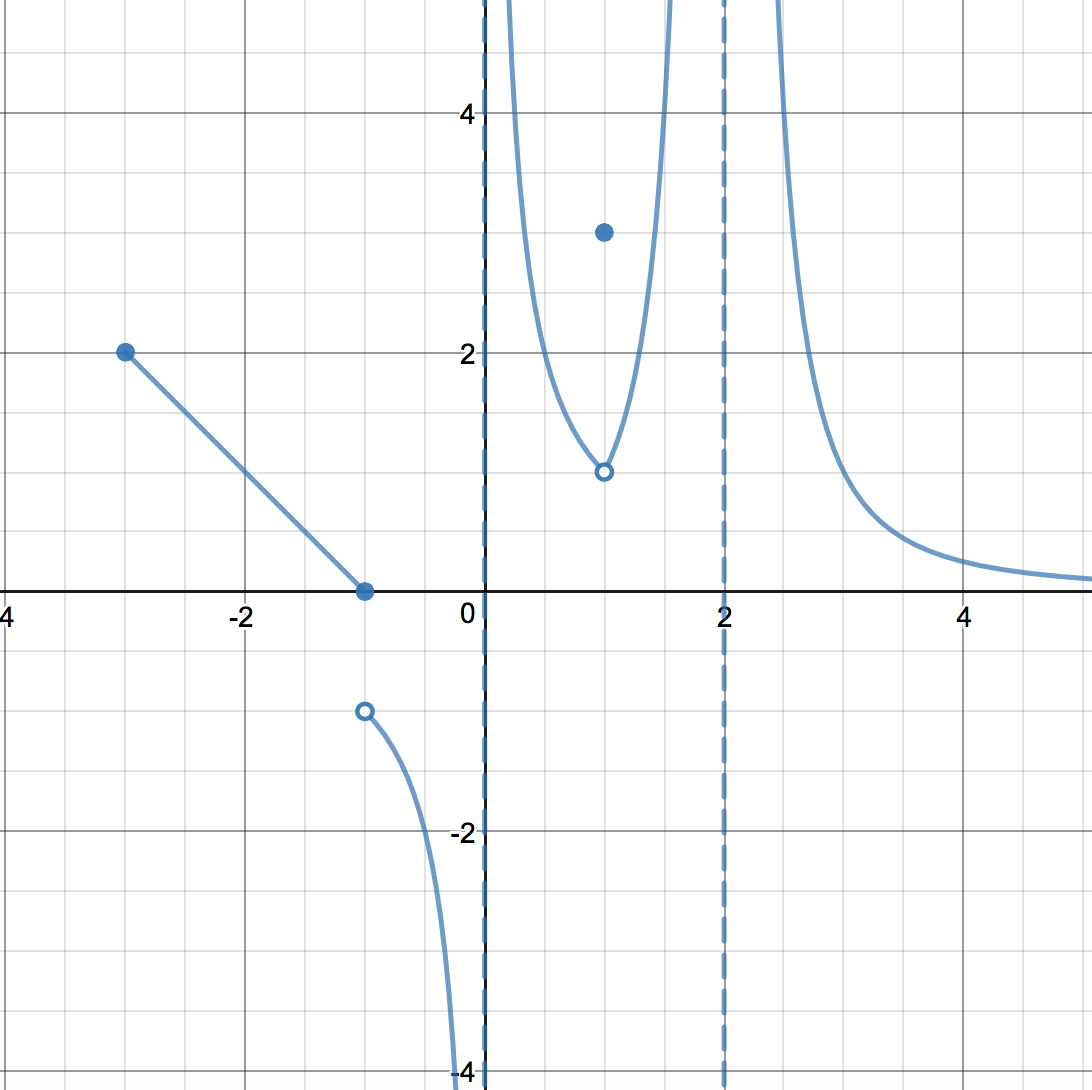
Evaluate $\lim _{x \to 3}\, [(x-1)^2-3]$ .

We will learn a quicker way to computing this limit in the next section, but for now, we have two approaches:

Using a graph. Let $f(x) = (x-1)^2-3$ . Which of the following represents the graph of $y = f(x)$ ?

Based on this graph, it appears that as $x$ gets closer to $3$ , the $y$ -values of $y = f(x)$ get closer to $\answer {1}$ .
Using a table. Using a calculator, fill in the following tables (round to four digits after the decimal point):
$\begin {array}{c|c} x & f(x) \\ \hline 3.1 & \answer {1.41} \\ 3.01 & \answer {1.0401} \\ 3.001 & \answer {1.004} \\ 3.0001 & \answer {1.0004} \\ \end {array}$

$\begin {array}{c|c} x & f(x) \\ \hline 2.9 & \answer {0.61} \\ 2.99 & \answer {0.9601} \\ 2.999 & \answer {0.996} \\ 2.9999 & \answer {0.9996} \\ \end {array}$
Based on these tables, we see that as the $x$ -values get closer to $3$ , the $y$ -values appear to be approaching $\answer {1}$ which doesdoes not match our answer using the graph above.

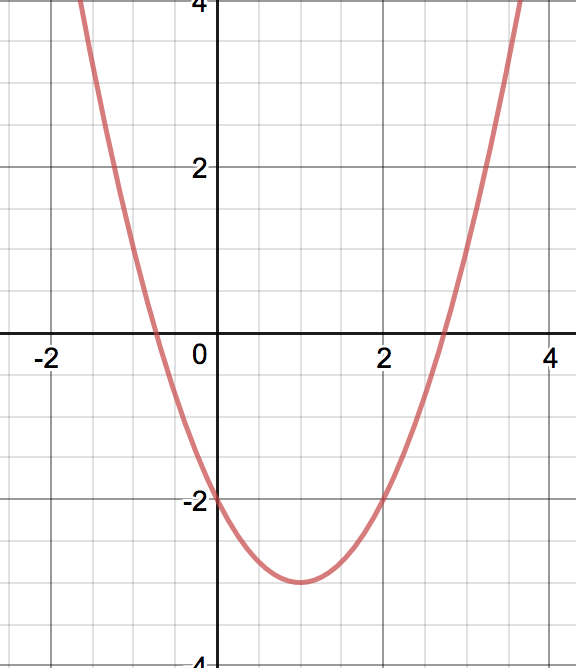
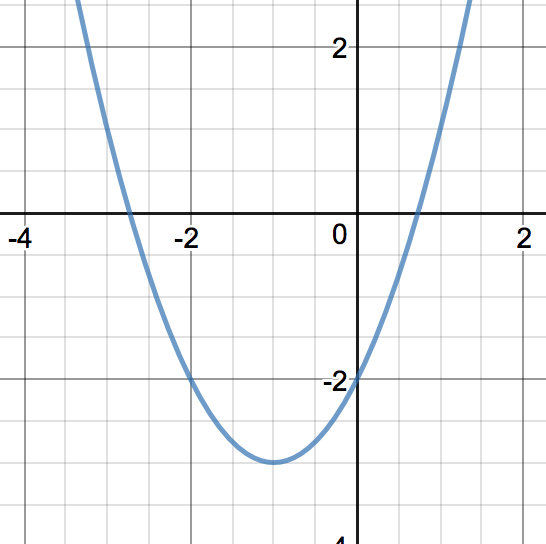
Calculate $\lim _{x \to 0} \frac {2\sin (x)}{x}$ .

Again, let’s look at both approaches.

Using a graph. The graph of $y = \frac {\sin (x)}{x}$ is shown below.

Notice that this function $f(x) =2 \sin (x)/x$ is undefined at $x=0$ , hence the hole at $x=0$ on the graph. However, as $x$ gets closer to $0$ , we note that the $y$ -values are getting closer to a certain value, and that value is $\answer {2}$ .
This problem illustrates the following: limits care about what is happening around a point, not necessarily what happens at that point.
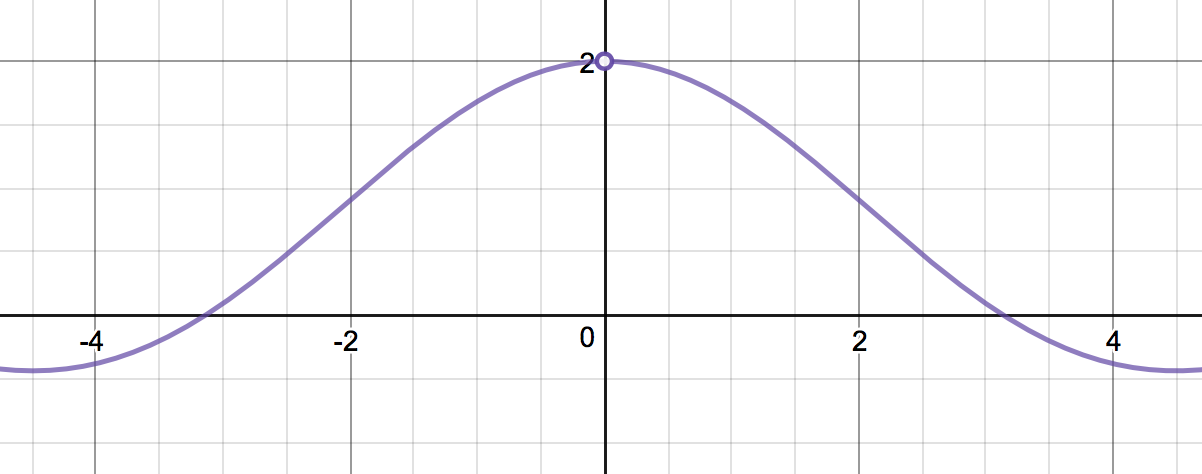
Using a table. Here is a table showing the values of $f(x)$ for different $x$ -values:
$\begin {array}{c|c} x & f(x) \\ \hline .5 & 1.9177 \\ .1 & 1.99667 \\ .01 & 1.99997 \\ \end {array}$

$\begin {array}{c|c} x & f(x) \\ \hline -.5 & 1.9177 \\ -.1 & 1.99667 \\ -.01 & 1.99997 \\ \end {array}$
Based on these tables, we see that as the $x$ -values get closer to $0$ , the $y$ -values appear to be approaching $\answer {2}$ which doesdoes not match our answer using the graph above.

Consider the following graph of a function $f(x)$ :

Evaluate the following (if they exist). If the quantity does not exist, enter DNE.

$f(-1) = \answer {2}$ .
$\lim _{x \to -1^-} f(x) = \answer {1}$ .
$\lim _{x \to -1^+} f(x) = \answer {2}$ .
Because $\lim _{x \to -1^-} f(x)$ $\lim _{x \to -1^+} f(x)$ , the limit $\lim _{x \to -1} f(x)$ existsdoes not exist .
$f(2) = \answer {1}$ .
$\lim _{x \to 2^-} f(x) = \answer {2}$ .
$\lim _{x \to 2^+} f(x) = \answer {2}$ .
$\lim _{x \to 2} f(x) = \answer {2}$ .
$f(4) = \answer {1}$ .
$\lim _{x \to 4^-} f(x) = \answer {1}$ .
$\lim _{x \to 4^+} f(x) = \answer {1}$ .
$\lim _{x \to 4} f(x) = \answer {1}$ .

Consider the following graph of a function $f(x)$ :

Evaluate the following (if they exist). If the quantity does not exist, enter DNE. If the limit is infinite, write “infinity” (or ”-infinity” for $-\infty$ ).

$\lim _{x \to 2^-} f(x) = \answer {\infty }$ .
$\lim _{x \to 2^+} f(x) = \answer {\infty }$ .
$\lim _{x \to 2} f(x) = \answer {\infty }$ .
$\lim _{x \to 1^+} f(x) = \answer {1}$ .
$\lim _{x \to 1} f(x) = \answer {1}$ .
$\lim _{x \to 0^-} f(x) = \answer {-\infty }$ .
$\lim _{x \to 0^+} f(x) = \answer {\infty }$ .
$\lim _{x \to 0} f(x) = \answer {DNE}$ .
$\lim _{x \to -1} f(x) = \answer {DNE}$ .
$\lim _{x \to -3^+} f(x) = \answer {2}$ .