As the number of seconds elapsed since the man
threw the baseball increases, the ball’s vertical distance from its initial position
increases. As the number of seconds elapsed since the man threw the baseball
increases, the ball’s vertical distance from its initial position decreases. For
equal changes in the number of seconds elapsed since the man threw the
baseball, the ball’s vertical distance from its initial position changes by equal
amounts. For successive uniform changes in the number of seconds elapsed
since the man threw the baseball, the ball’s vertical distance from its initial
position changes by increasing amounts. For successive uniform changes in
the number of seconds elapsed since the man threw the baseball, the ball’s
vertical distance from its initial position changes by decreasing amounts.
Please answer each of these questions to the best of your ability. You are welcome to re-watch parts of any of the videos to help you. Select the answer which best represents the way you think about the setting (multiple answers may be correct).
A man throws a baseball horizontally off of the top of a building. Which of the
following statements most accurately represents the relationship between the ball’s
vertical distance from its initial position (in feet) and the number of seconds elapsed
since the man threw the baseball?
Imagine the bottle below being filled with water. Which of the following statements
most accurately represents the relationship between the volume of water in
the bottle and the distance from the surface of the water to the top of the
bottle?
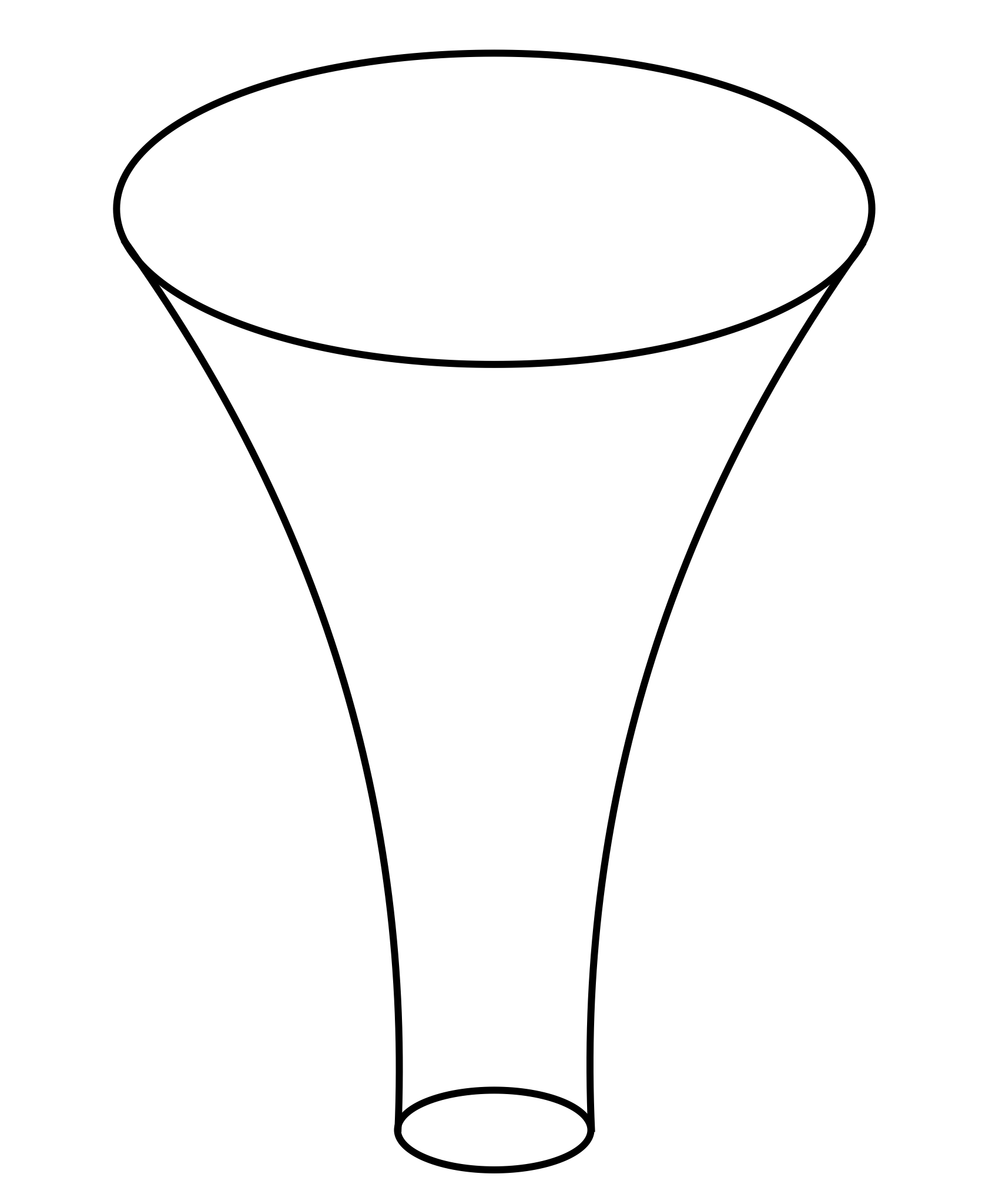

As the volume of water in the bottle increases, the distance from the surface of the
water to the top of the bottle decreases. For successive uniform changes in the
volume of water in the bottle, the distance from the surface of the water to
the top of the bottle changes by increasing amounts. As the volume of
water in the bottle increases, the distance from the surface of the water to
the top of the bottle increases. For successive uniform changes in the
volume of water in the bottle, the distance from the surface of the water
to the top of the bottle changes by decreasing amounts. For successive
uniform changes in the volume of water in the bottle, the distance from the
surface of the water to the top of the bottle changes by equal amounts.