Pre-Video Questions

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

To go back to the list of video sets, click HERE.

Before watching the videos, think about and answer these questions to the best of your ability.

The velocity of a runner at different moments in time since starting a race is given by the following table.


t in seconds	2	4	6	8	10

v(t) in m/s	1	3	5	6	6

Based on the table, which of the following is an approximation to $\int _4^8 v(t) dt$ ?

$18$ meters $28$ meters $30$ meters $42$ meters $44$ meters None of the above

Use the graph of the rate, $y = R(t)$ , to answer the following question:

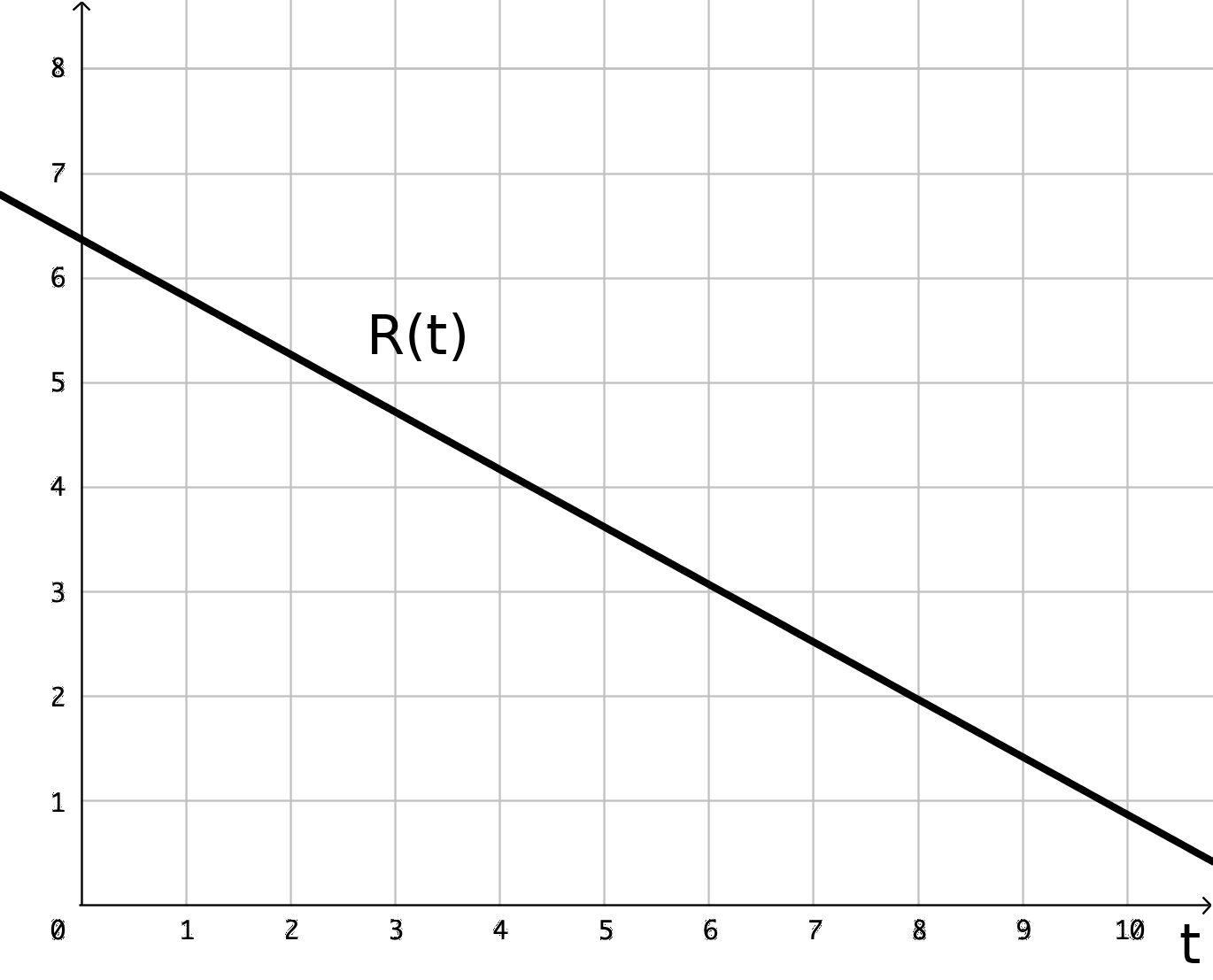
Which value is greatest?

$\int _2^8 R(t) dt$ $\int _3^9 R(t) dt$ $\sum _{k=0}^2 R(2+ k \times \Delta t)\times \Delta t$ where $\Delta t = 2$ $\sum _{k=0}^2 R(2+ k \times \Delta t)\times \Delta t$ where $\Delta t = 1$ None of the above More information is needed

The following picture illustrates a Riemann sum using $n$ terms. The dotted lines are located at $x_0$ , $x_1$ , etc.

Which expression from the Riemann Sum definition of the definite integral represents the green shaded region?

$\sum _{k=0}^{n-1} f(x_k) \Delta x$ $\int _a^b f(x) dx$ $f(x_2)$ $\Delta x$ $f(x_2) \Delta x$ $\lim _{n \to \infty } \sum _{k=0}^{n-1} f(x_k) \Delta x$

Overall, how confident are you in your answers?

Not at all confident Not very confident Somewhat confident Very Confident