Please answer each of these questions to the best of your ability. You are welcome to re-watch parts of any of the videos to help you. Select the answer which best represents the way you think about the setting.

A man throws a baseball horizontally off of the top of a building. Which of the following statements accurately represent the relationship between the ball’s vertical distance from its initial position at the top of the building and the number of seconds elapsed since the man threw the baseball? Select the answer which correctly communicates the most information.
As the number of seconds elapsed since the man threw the baseball increases, the ball’s vertical distance from its initial position increases. As the number of seconds elapsed since the man threw the baseball increases, the ball’s vertical distance from its initial position decreases. For successive uniform changes in the number of seconds elapsed since the man threw the baseball, the ball’s vertical distance from its initial position changes by equal amounts. For successive uniform changes in the number of seconds elapsed since the man threw the baseball, the ball’s vertical distance from its initial position changes by increasing amounts. For successive uniform changes in the number of seconds elapsed since the man threw the baseball, the ball’s vertical distance from its initial position changes by decreasing amounts.
Imagine the bottle below being filled with water. Which of the following statements accurately represents the relationship between the volume of water in the bottle and the distance from the surface of the water to the top of the bottle? Select the answer which correctly communicates the most information.
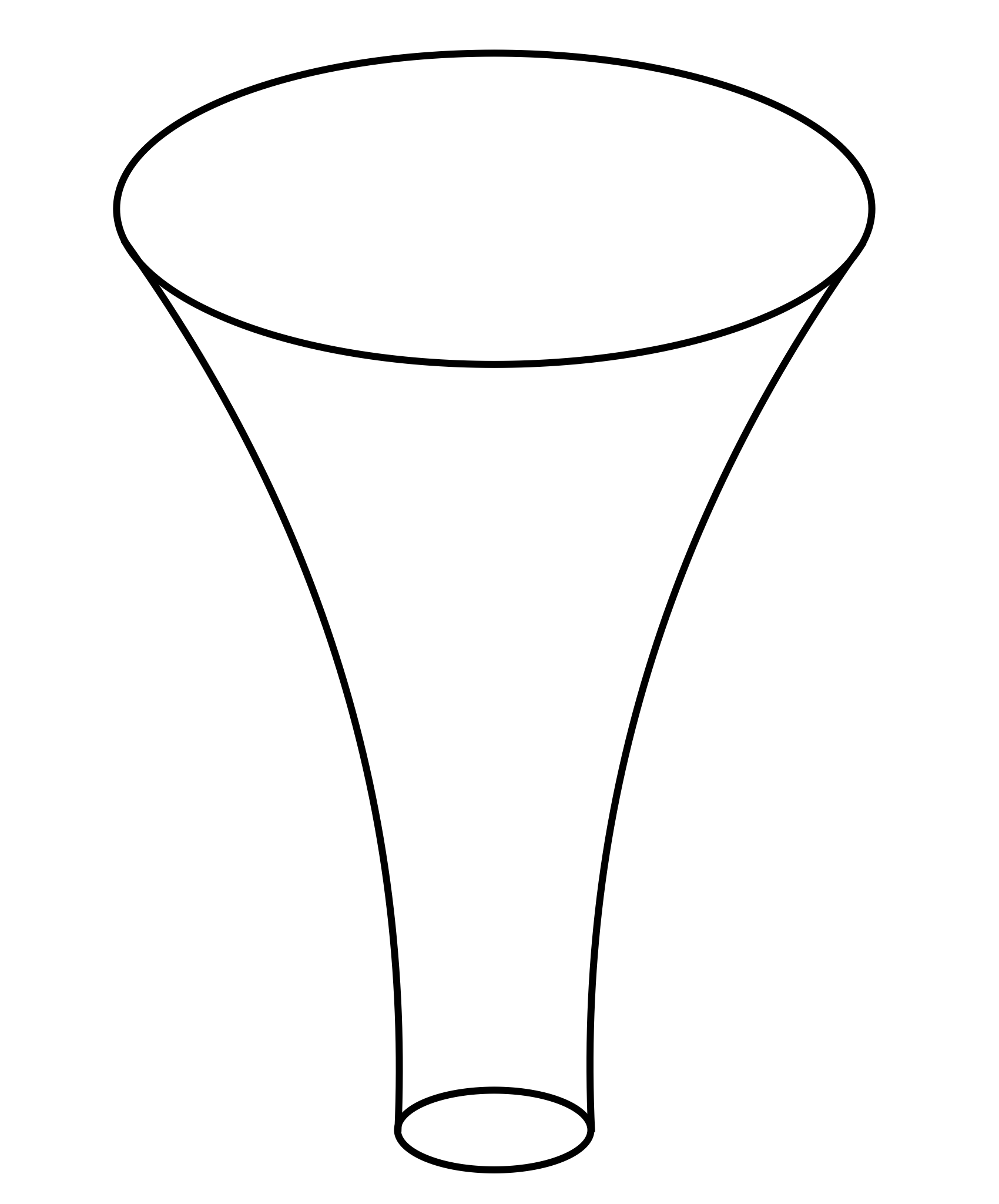
As the volume of water in the bottle increases, the distance from the surface of the water to the top of the bottle decreases. As the volume of water in the bottle increases, the distance from the surface of the water to the top of the bottle increases. For successive uniform changes in the volume of water in the bottle, the distance from the surface of the water to the top of the bottle changes by increasing amounts. For successive uniform changes in the volume of water in the bottle, the distance from the surface of the water to the top of the bottle changes by decreasing amounts. For successive uniform changes in the volume of water in the bottle, the distance from the surface of the water to the top of the bottle changes by equal amounts.