Video Set Introduction

$\newenvironment {prompt}{}{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1}$ $% This file was *autogenerated* from intro.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %13d7bcab4dec66c30998eccbbe6b6497% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

Before watching the video, think about and answer these questions to the best of your ability. Your answer will always be recorded as correct, regardless of your answer choice.

Consider the function $f(x) = -x^{2.2}+3x^{1.2}+2$ . Use calculus to find the maximum value of $f(x)$ over the interval $[-.75,4]$ . $\answer [format=string,validator=nameCheck]{}$

Consider the graph below. This is the graph of $f'(x)$ , the derivative of the function $f(x)$ . The labels are naming the $x$ -coordinate of each point. The function is not defined for $x$ -values less than 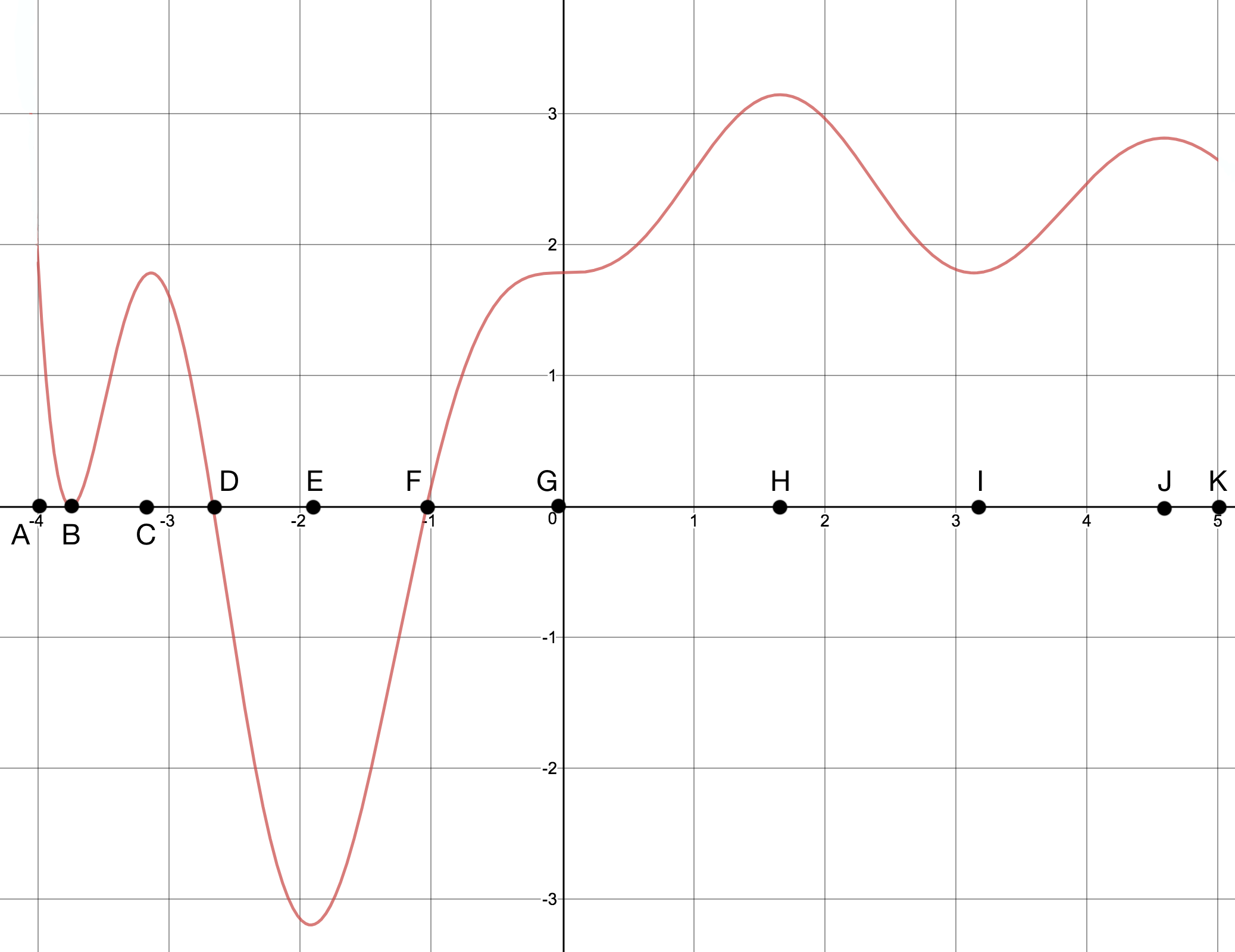$x=A$ .

In particular, note that:

from $x=A$ to $x=B$ , $f'(x)>0$
from $x=B$ to $x=C$ , $f'(x)>0$
from $x=C$ to $x=D$ , $f'(x)>0$
from $x=D$ to $x=E$ , $f'(x)<0$
from $x=E$ to $x=F$ , $f'(x)<0$
from $x=F$ to $x=G$ , $f'(x)>0$
from $x=G$ to $x=H$ , $f'(x)>0$
from $x=H$ to $x=I$ , $f'(x)>0$
from $x=I$ to $x=J$ , $f'(x)>0$

For each of the points, determine whether they are a maximum, minimum, or neither.

At $x=A$ , f(x) has a maximum minimum neither	At $x=B$ , f(x) has a maximum minimum neither	At $x=C$ , f(x) has a maximum minimum neither	At $x=D$ , f(x) has a maximum minimum neither	At $x=E$ , f(x) has a maximum minimum neither
At $x=F$ , f(x) has a maximum minimum neither	At $x=G$ , f(x) has a maximum minimum neither	At $x=H$ , f(x) has a maximum minimum neither	At $x=I$ , f(x) has a maximum minimum neither	At $x=J$ , f(x) has a maximum minimum neither