Vector fields

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\,d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

We introduce the idea of a vector at every point in space.

Types of functions

When we started on our journey exploring calculus, we investigated functions $f:\R \to \R$ . Typically, we interpret these functions as being curves in the $(x,y)$ -plane:

We’ve also studied vector-valued functions $\vec {f}:\R \to \R ^n$ . We can interpret these functions as parametric curves in space:

We’ve also studied functions of several variables $F:\R ^n \to \R$ . We can interpret these functions as surfaces in $\R ^{n+1}$ . For example if $n=2$ , then $F:\R ^2\to \R$ plots a surface in $\R ^3$ :

Now we are ready for a new type of function.

Vector fields

Now we will study vector-valued functions of several variables: $\vec {F}:\R ^n\to \R ^n$ We interpret these functions as vector fields, meaning for each point in the $(x,y)$ -plane we have a vector.

To some extent functions like this have been around us for a while, for if $G:\R ^n\to \R$ then $\grad G$ is a vector-field. Let’s be explicit and write a definition.

A vector field in $\R ^n$ is a function $\vec {F}: \R ^n\to \R ^n$ where for every point in the domain, we assign a vector to the range.

Consider the following table describing a vector field $\vec {F}$ :

What is $\vec {F}(1,7)$ ? $\vec {F}(1,7) = \vector {\answer {1},\answer {-1}}$

What is $\vec {F}(3,5)$ ? $\vec {F}(3,5) = \vector {\answer {0},\answer {2}}$

What is $\vec {F}(2,6)$ ? $\vec {F}(2,6) = \vector {\answer {0},\answer {0}}$

Consider the following picture:

Which vector field is illustrated by this picture?

$\vec {F}(x,y)=\vector {x,y/2}$ $\vec {F}(x,y)=1/2$ $\vec {F}(x,y)=x+y/2$ $\vec {F}(x,y)=\vector {1,1/2}$

Note that with the first choice, the lengths of the vectors is changing, and that does not appear to be the case with our vector field.

The second choice is not a vector field.

The third choice is not a vector field.

The fourth choice is a constant vector field, and is the correct answer.

Properties of vector fields

As we will see in the chapters to come, there are two important qualities of vector fields that we are usually on the look-out for. The first is rotation and the second is expansion. In the sections to come, we will make precise what we mean by rotation and expansion. In this section we simply seek to make you aware that these are the fundamental properties of vector fields.

Radial fields

Very loosely speaking a radial field is one where the vectors are all pointing toward a spot, or away from a spot. Let’s see some examples of radial vector fields.

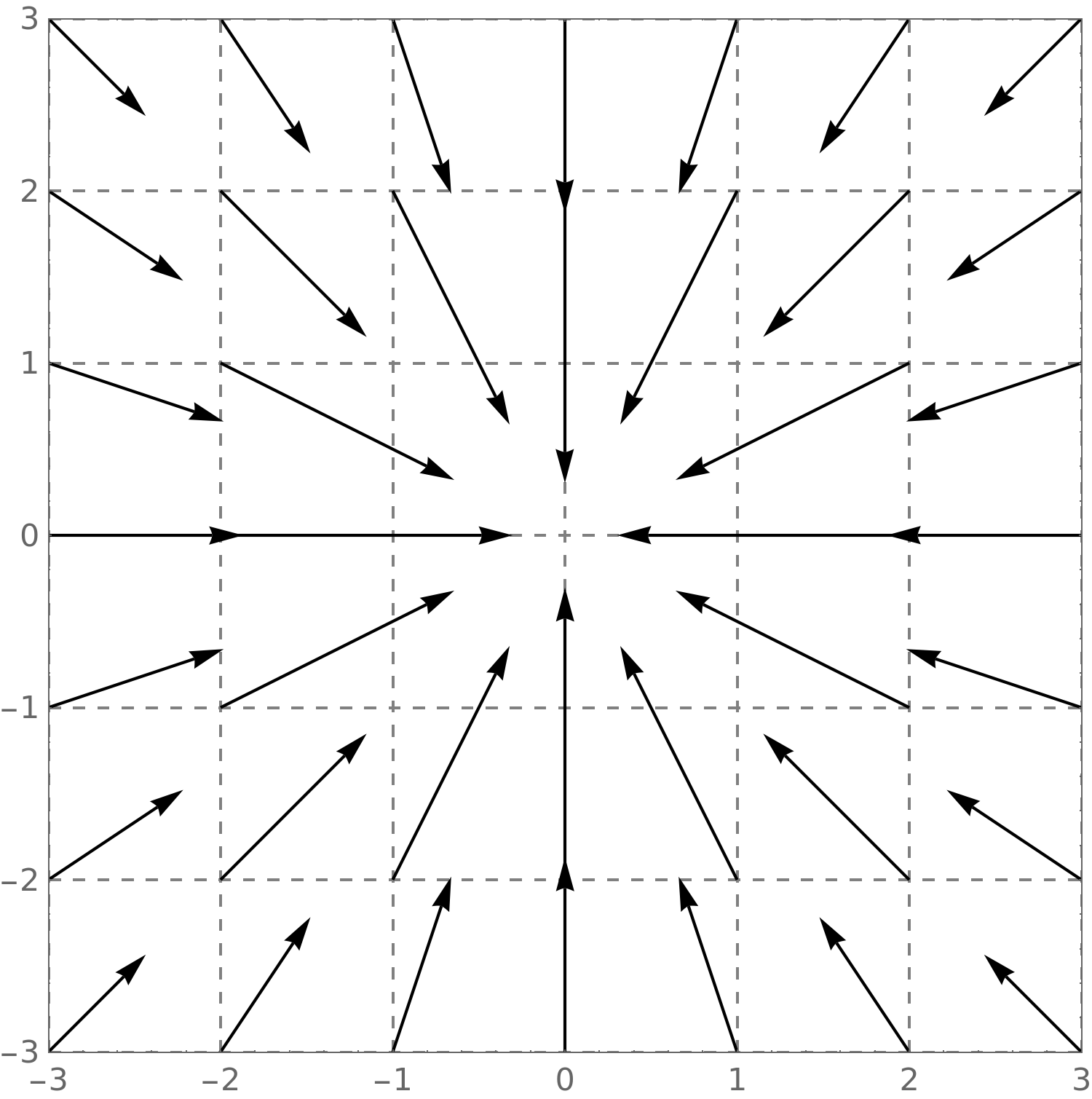
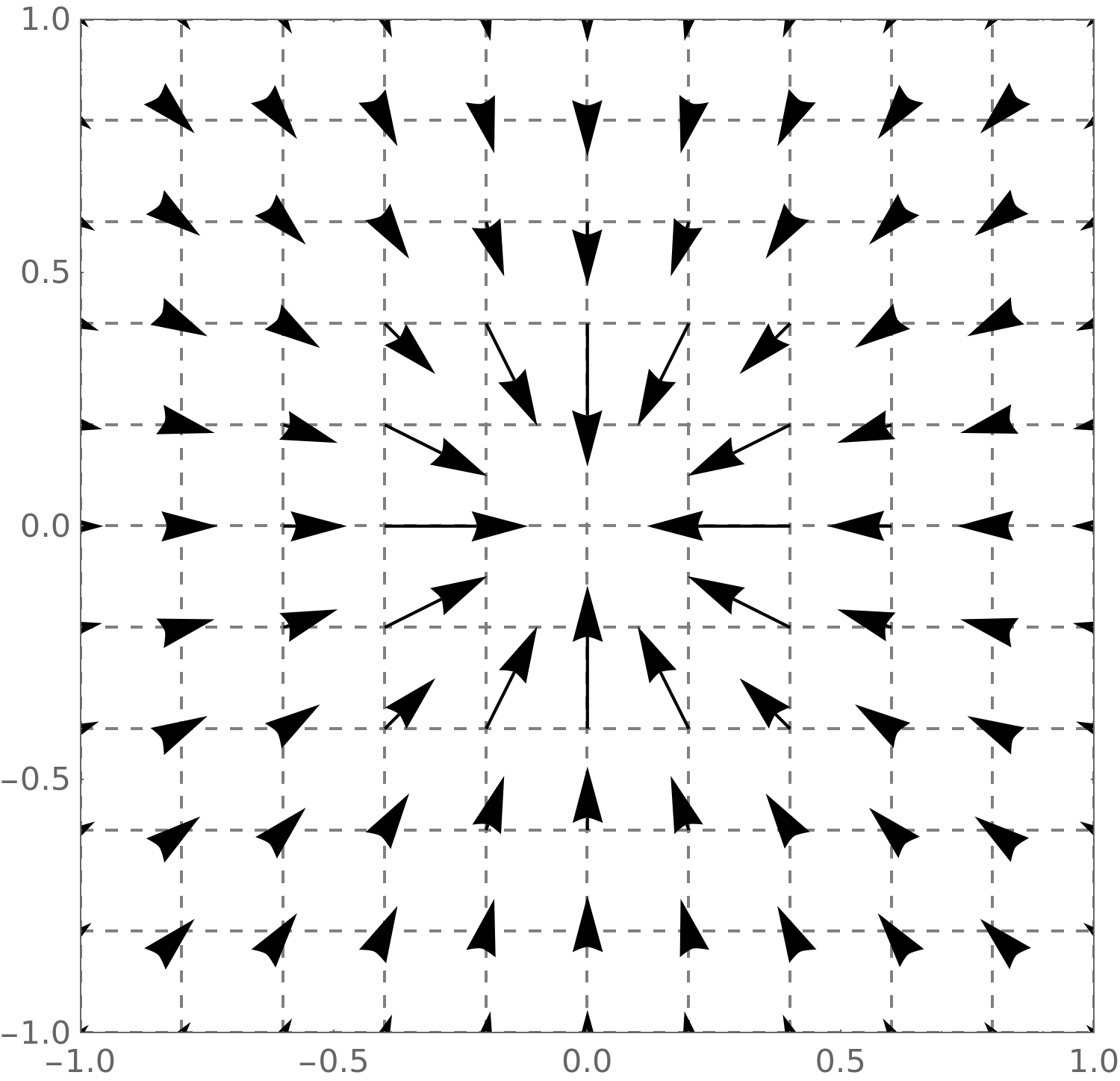
Here we see $\vec {F}(x,y) = \vector {\frac {x}{\sqrt {x^2+y^2}},\frac {y}{\sqrt {x^2+y^2}}}$ .

Those vectors are all pointing away from the central point!

Here we see $\vec {G}(x,y) = \vector {\frac {-x}{x^2+y^2},\frac {-y}{x^2+y^2}}$ .

Those vectors are all pointing toward the central point.

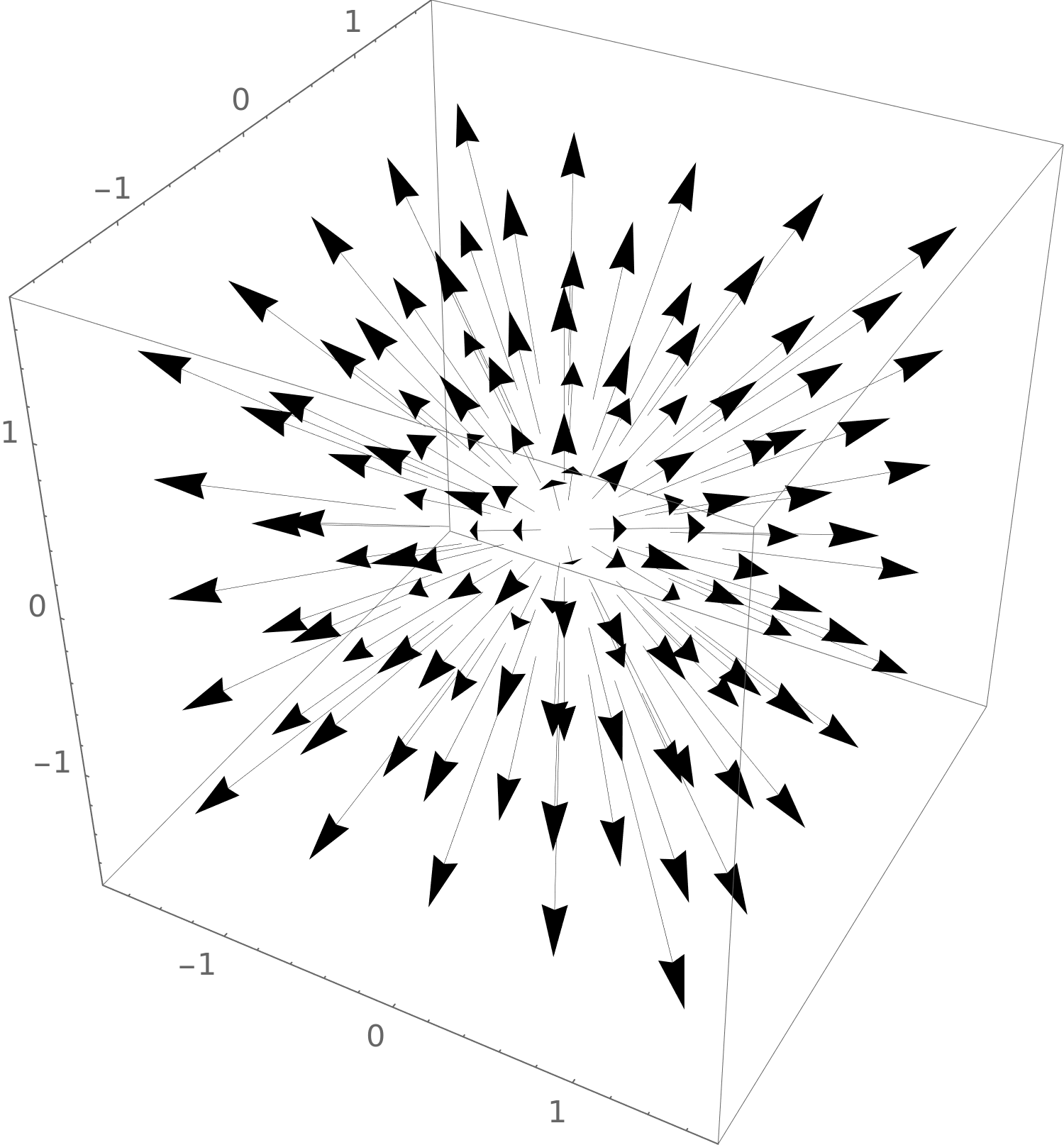
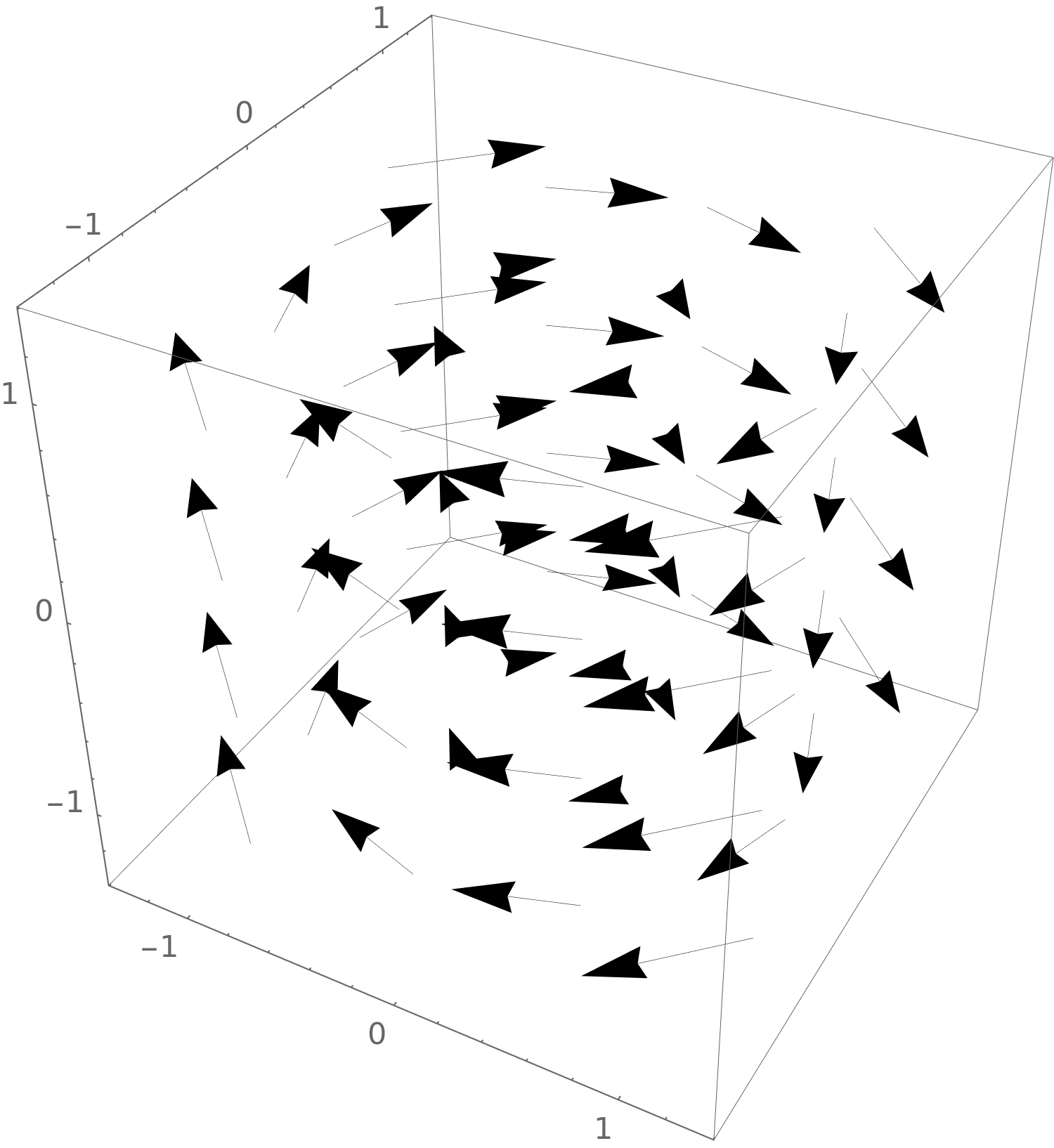
Here we see $\vec {H}(x,y,z) = \vector {x,y,z}$ .

This is a three-dimensional vector field where all the vectors are pointing away from the central point.

Each of the vector fields above is a radial vector field. Let’s give an explicit definition.

A radial vector field is a field of the form $\vec {F}:\R ^n\to \R ^n$ where $\vec {F}(\vec {x}) = \frac {\pm \vec {x}}{|\vec {x}|^p}$ where $p$ is a real number.

Fun fact: Newton’s law of gravitation defines a radial vector field.

Is $\vec {F}(x,y,z) = \vector {x,y,z}$ a radial vector field?

yes no

Absolutely! This vector field can be rewritten as: $\vector {\frac {x}{(\sqrt {x^2+y^2+z^2})^p},\frac {y}{(\sqrt {x^2+y^2+z^2})^p},\frac {z}{(\sqrt {x^2+y^2+z^2})^p}}$ where $p=\answer {0}$ .

Some fields look like they are expanding and are. Other fields look like the are expanding but they aren’t. In the sections to come, we’re going to use calculus to precisely define what we mean by a field “expanding.” This property will be called divergence.

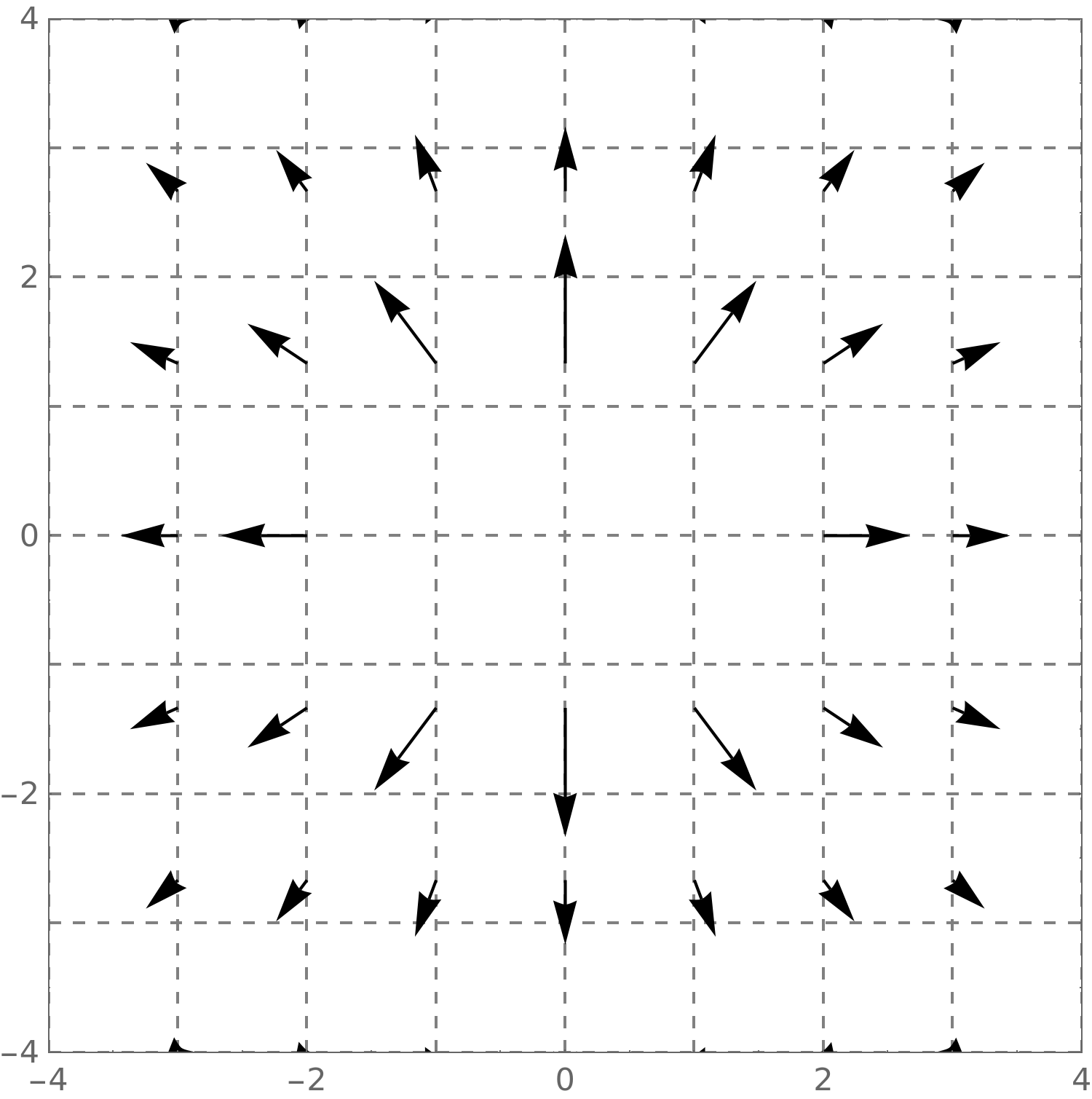
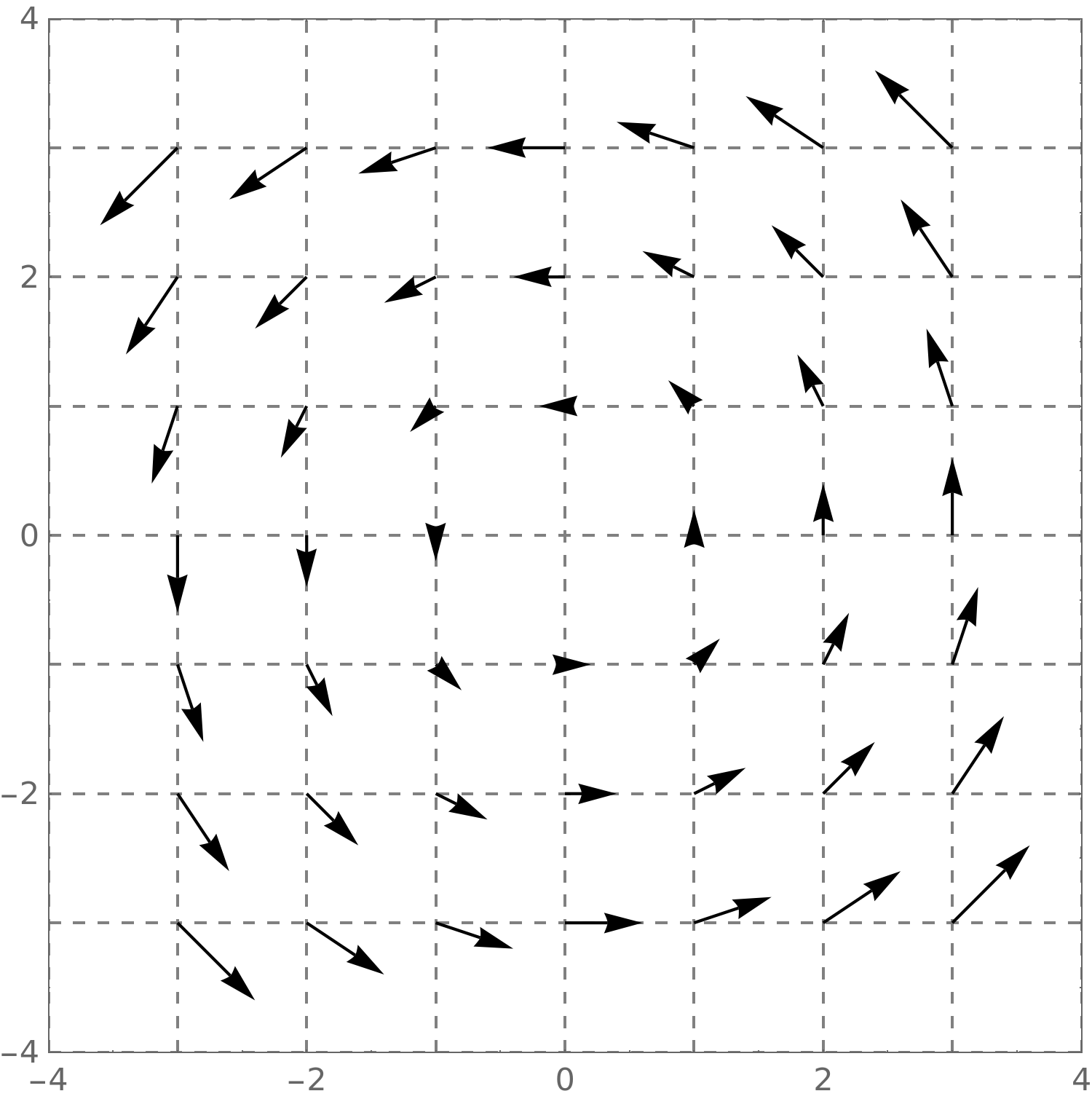
Rotational fields

Vector fields can easily exhibit what looks like “rotation” to the human eye. Let’s show you a few examples.

Here we see $\vec {F}(x,y) = \vector {-y,x}$ .

This vector field looks like it has counterclockwise rotation.

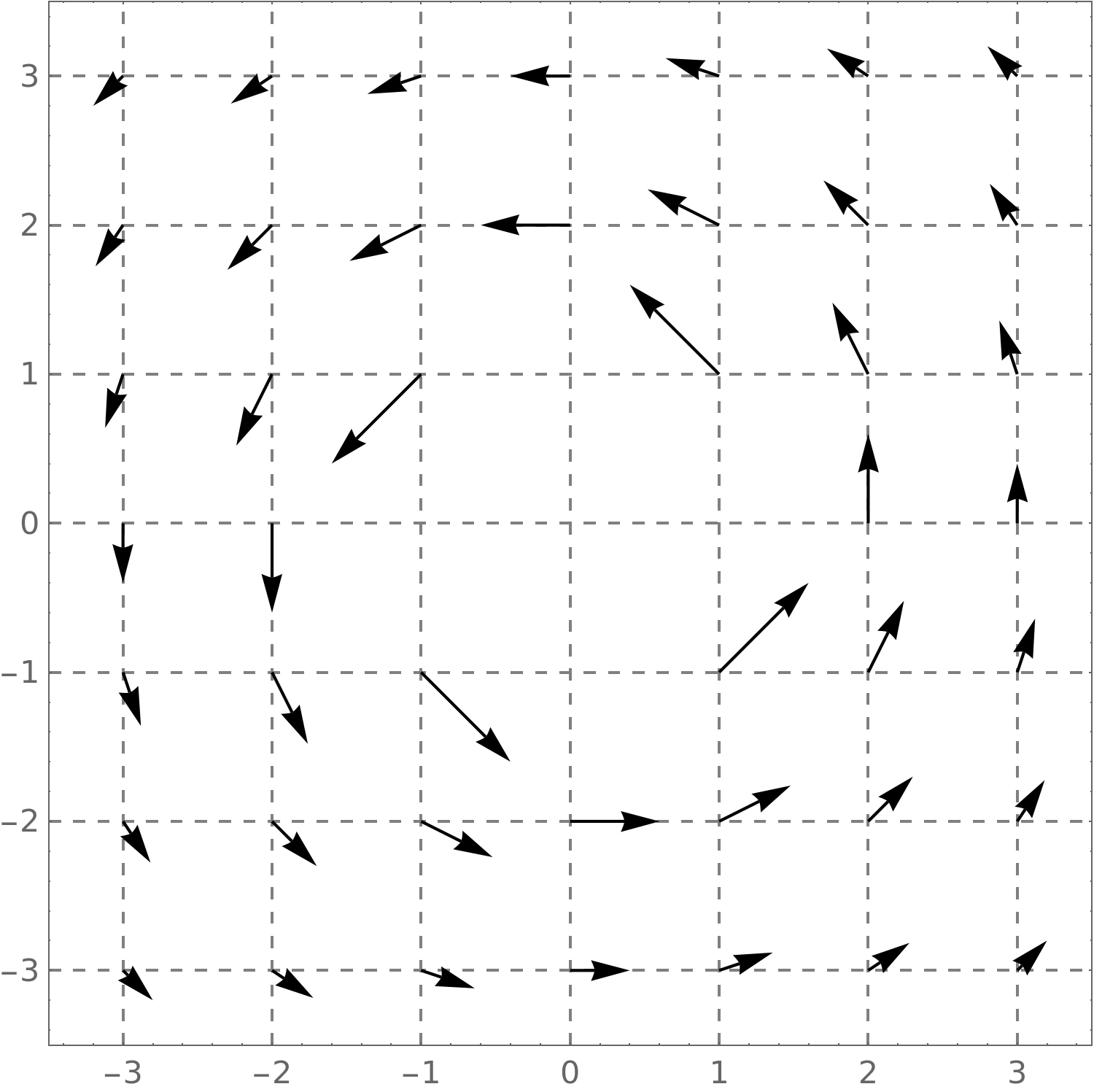
Here we see $\vec {F}(x,y) = \vector {\frac {-y}{x^2+y^2},\frac {x}{x^2+y^2}}:$

This vector field looks like it has clockwise rotation.

At this point, we’re going to give some “spoilers.” It turns out that from a local perspective, meaning looking at points very very close to each other, only the first example exhibits “rotation.” While the second example looks like it is “rotating,” as we will see, it does not exhibit “local rotation.” Moreover, in future sections we will see that rotation (even local rotation) in three-dimensional space must always happen around some “axis” like this:

In the sections to come, we will use calculus to precisely explain what we mean by “local rotation.” This property will be called curl.

Gradient fields

In this final section, we will talk about fields that arise as the gradient of some differentiable function. As we will see in future sections, these are some of the nicest vector fields to work with mathematically.

Consider any differentiable function $F:\R ^n\to \R$ . A gradient field is a vector field $\vec {G}:\R ^n\to \R ^n$ where $\vec {G} = \grad F.$ Note, since we are assuming $F$ is differentiable, we are also assuming that $\vec {G}$ is defined for all points in $\R ^n$ .

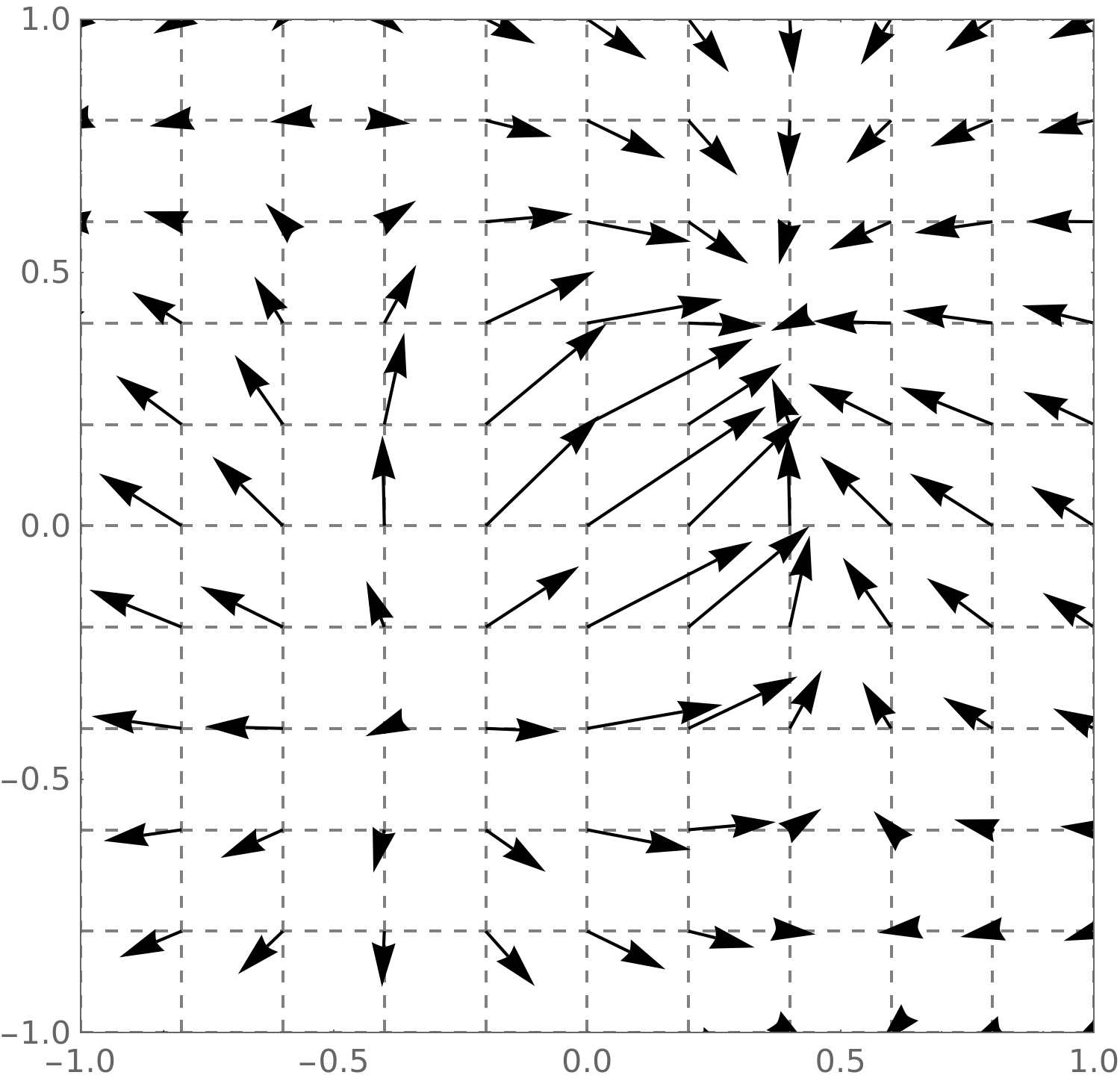
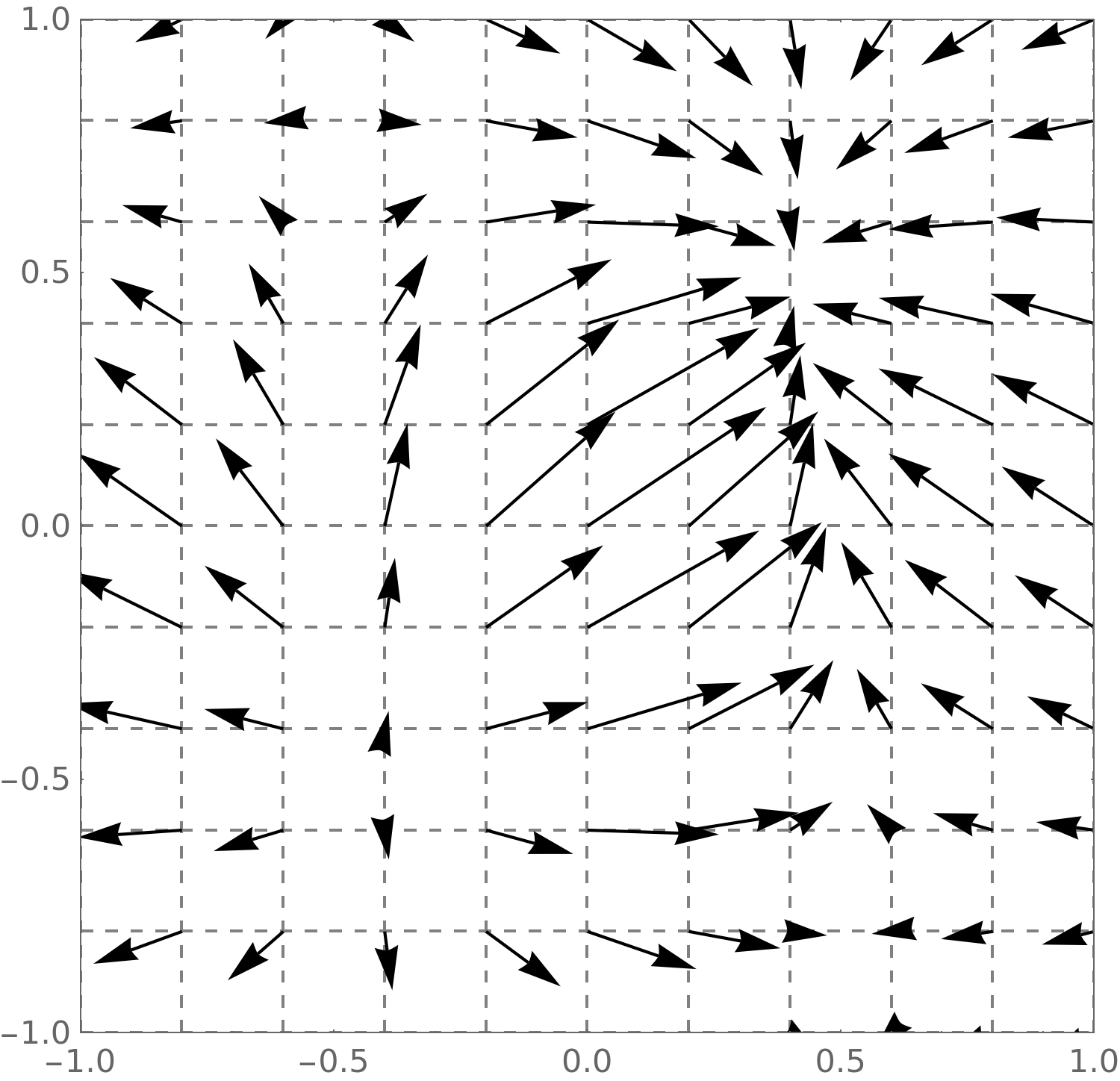
Let’s take a look at a gradient field.

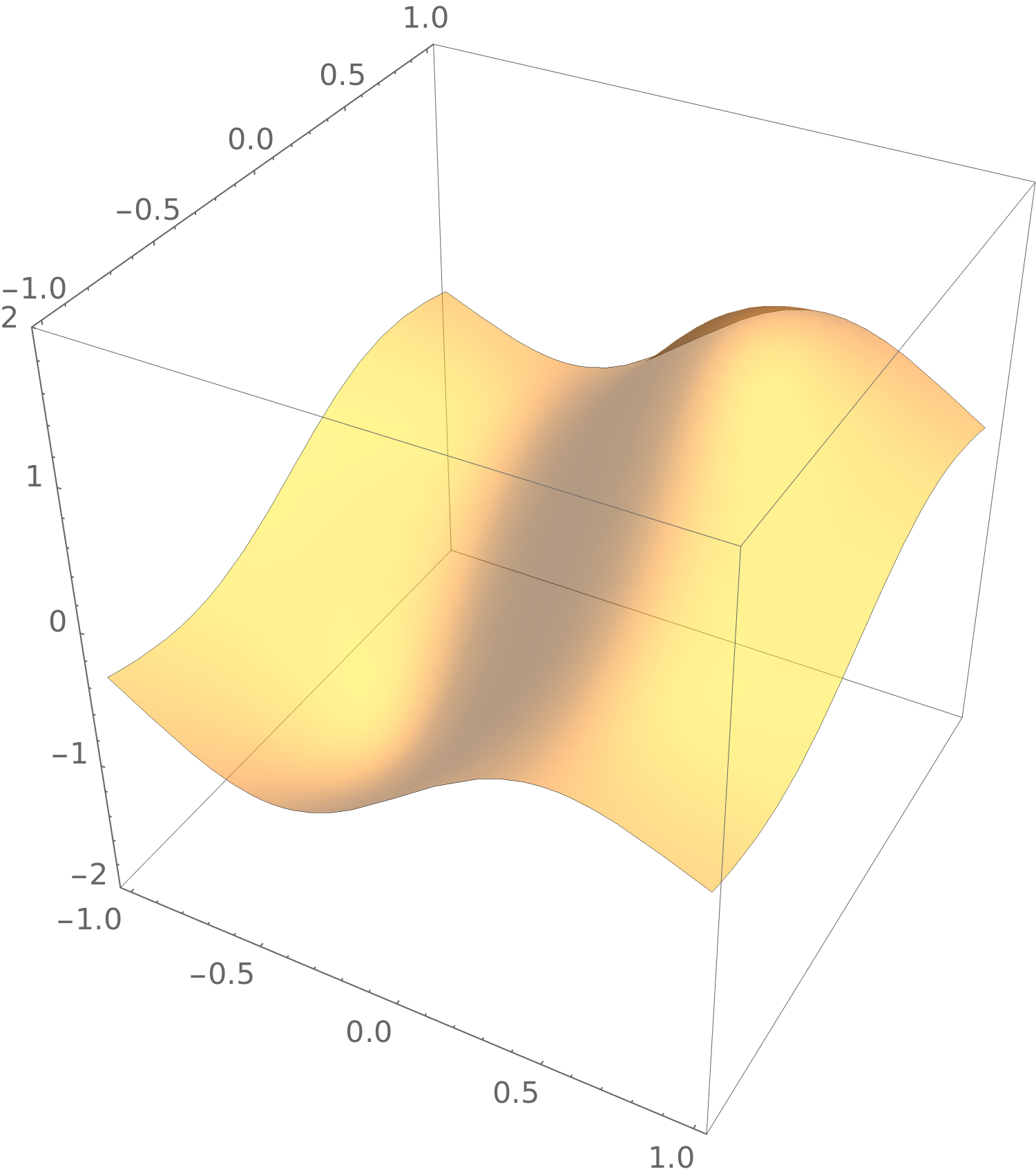
Consider $F(x,y) = \frac {\sin (3x)+\sin (2y)}{1+x^2+y^2}$ . A plot of this function looks like this:

The gradient field of $F$ looks like this:

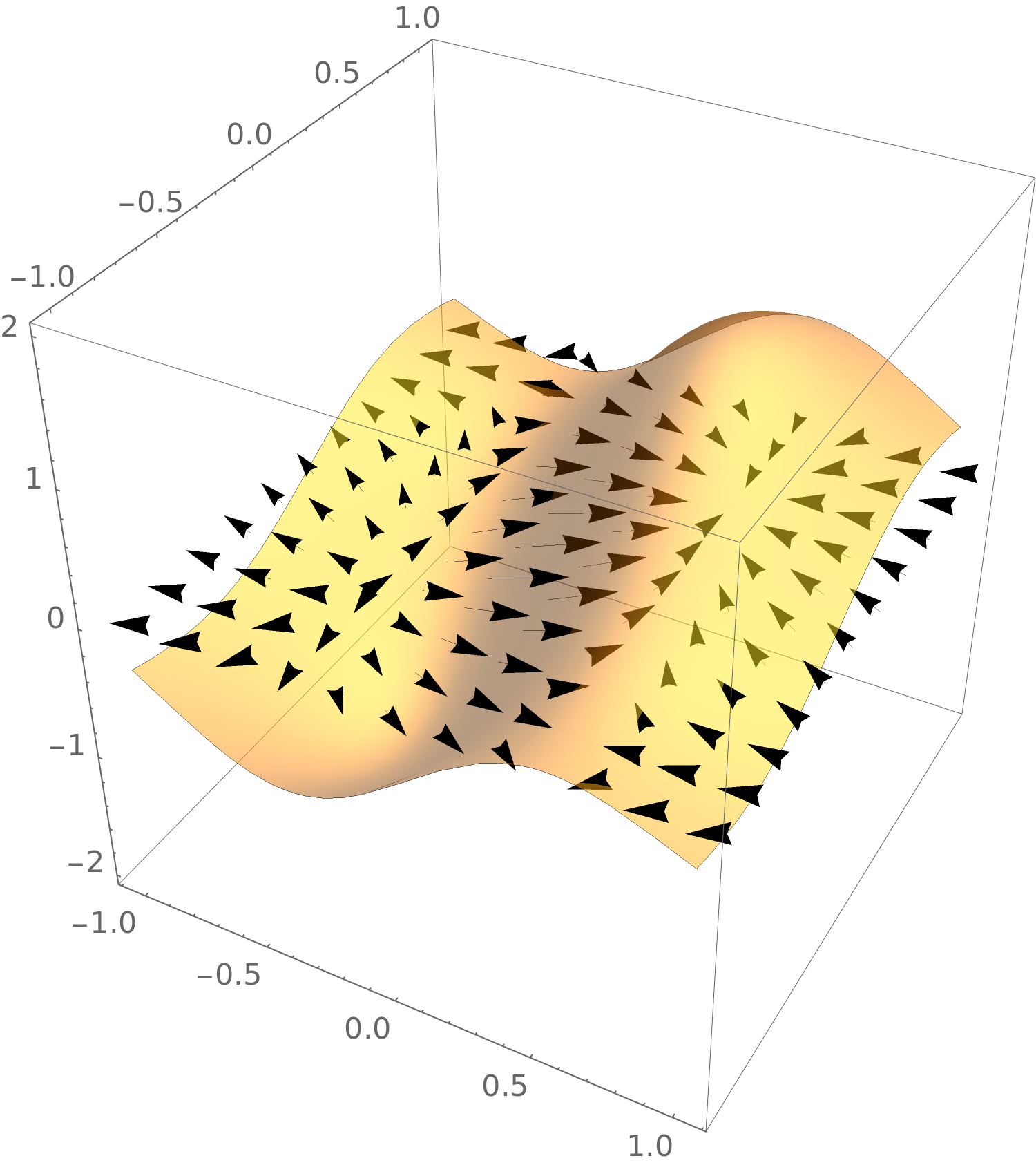
Note we can see the vector pointing in the initial direction of greatest increase. Let’s see a plot of both together:

Remind me, what direction do gradient vectors point?

Gradient vectors point to the maximum. Gradient vectors point up. Gradient vectors point in the initial direction of greatest increase.

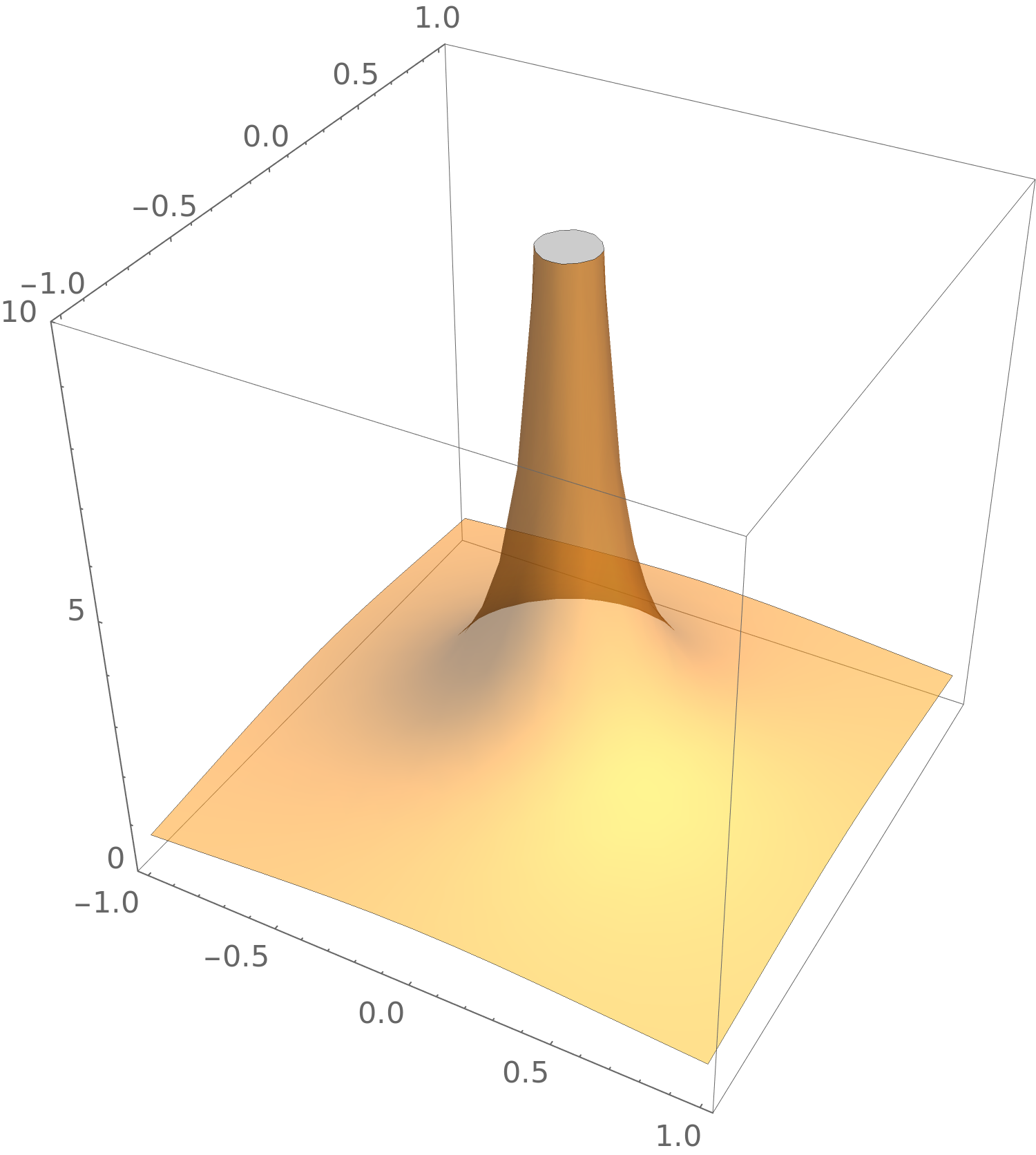
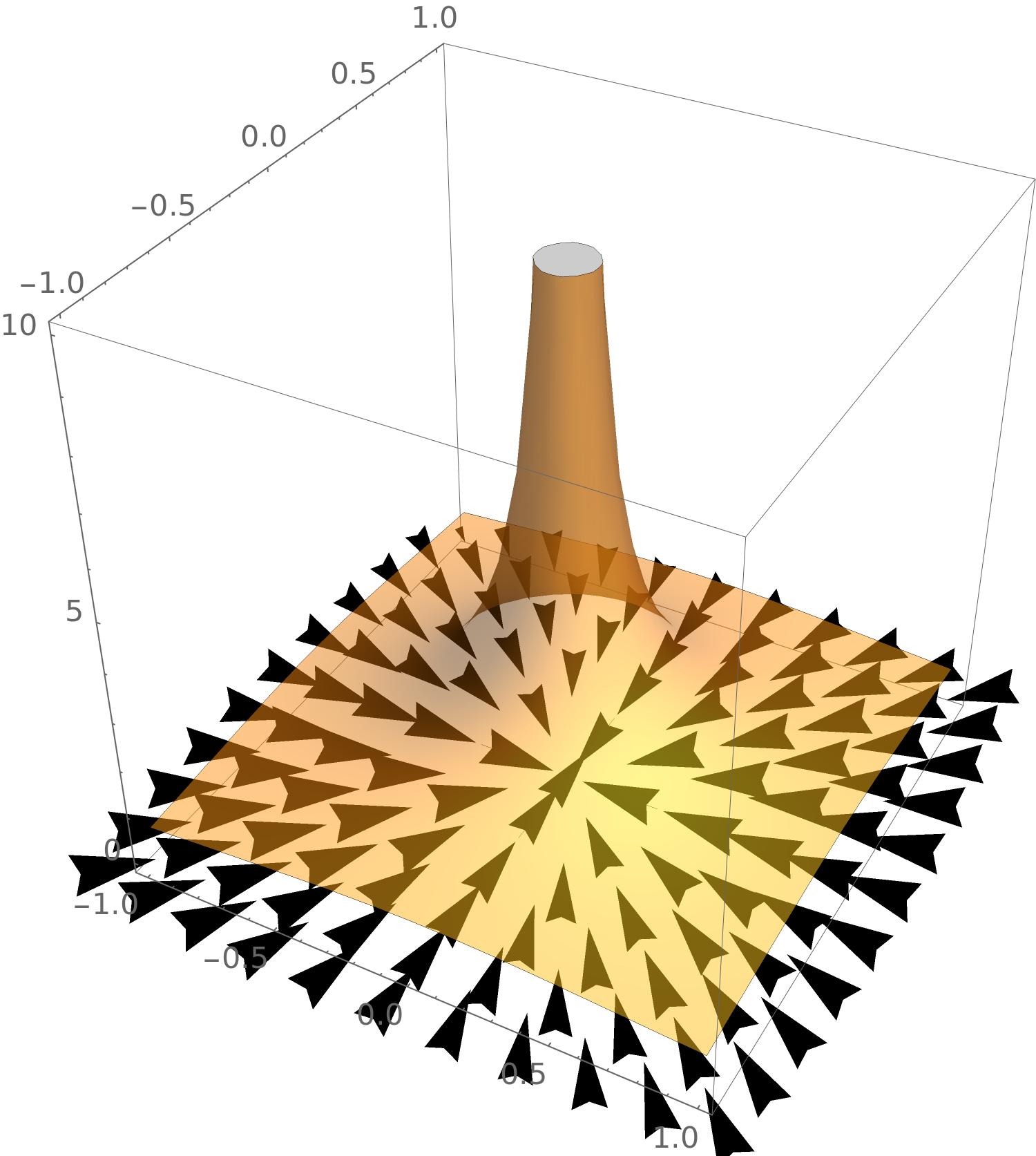
Now consider $F(x,y) = \frac {1}{\sqrt {x^2+y^2}}$ . A plot of this function looks like this:

The gradient field of $F$ $\grad F(x,y) = \vector {\frac {-x}{(x^2+y^2)^{3/2}},\frac {-y}{(x^2+y^2)^{3/2}}}$ looks like this:

Note we can see the vector pointing in the initial direction of greatest increase. Let’s see a plot of both together:

The shape of things to come

Now we present the beginning of a big idea. By the end of this course, we hope to give you a glimpse of “what’s out there.” For this we’re going to need some notation. Think of $A$ and $B$ as sets of numbers, like $A=\R$ or $A=\R ^n$ or $B=\R$ or $B=\R ^n$ .

$C(A,B)$ is the set of continuous functions from $A$ to $B$ .
$C^1(A,B)$ is the set of differentiable functions from $A$ to $B$ whose first-derivative is continuous.
$C^2(A,B)$ is the set of differentiable functions from $A$ to $B$ whose first and second derivatives are continuous.
$C^n(A,B)$ is the set of differentiable function from $A$ to $B$ where the first $n$ th derivatives are continuous.
$C^\infty (A,B)$ is the set of differentiable functions from $A$ to $B$ where all of the derivatives are continuous.

Here is a deep idea:

The gradient turns functions of several variables into vector fields.

We can write this with our new notation as: $C^\infty (\R ^n,\R )\overset {\grad }{\to }C^\infty (\R ^n,\R ^n)$

The Clairaut gradient test

Now we give a method to determine if a field is a gradient field.

Clairaut A vector field $\vec {G}(x,y) = \vector {M(x,y),N(x,y)}$ , where $M$ and $N$ have continuous partial derivatives, is a gradient field if and only if $\pp [N]{x} -\pp [M]{y} = 0$ for all $x$ and $y$ .

Let’s take a second and think about the gradient as a function on functions. Let $C^\infty (A,B)$ be the set of all function from $A$ to $B$ whose $i$ th-derivatives are continuous for all values of $i$ . The gradient takes functions of several variables and maps them to vector fields:

So $\vec {G}(x,y) = \vector {M(x,y),N(x,y)}$ if and only if there is some function $F:\R ^2\to \R$ where $\pp [F]{x} = M \quad \text {and}\quad \pp [F]{y} = N$ but if all the partial derivatives are continuous, then: $\pp [M]{y} = \frac {\partial ^2 F}{\partial y\partial x} = \frac {\partial ^2 F}{\partial x\partial y} = \pp [N]{x}$ This is true if and only if $\pp [N]{x} -\pp [M]{y} = 0$ .

If $\vec {G} = \grad F$ , then $F$ is called a potential function for $\vec {G}$ .

Is $\vec {G} = \vector {2x+3y,2+3x+2y}$ a gradient field? If so find a potential function.

To start, let’s do Clairaut’s gradient test: $\begin{align*} M(x,y) &= \answer[given]{2x+3y}\\ N(x,y) &= \answer[given]{2+3x+2y} \end{align*}$ And so $\begin{align*} \pp[N]{x} &= \answer[given]{3} \pp[M]{y} &= \answer[given]{3} \end{align*}$ And so we see $\pp [N]{x} -\pp [M]{y} = 0$ , and thus $\vec {G}$ is a gradient field. Now let’s try to find a potential function. To do this, we’ll antidifferentiate—in essence we want to “undo” the gradient. Write with me: $\begin{align*} \int M(x,y) \d x &= \int \left(\answer[given]{2x+3y}\right) \d x \\ &= \answer[given]{x^2+3xy} + c(y) \end{align*}$ where $C(y)$ is a function of $y$ . In a similar way: $\begin{align*} \int N(x,y) \d y &= \int \left(\answer[given]{2+3x+2y}\right) \d y \\ &= \answer[given]{2y + 3xy+ y^2} + k(x) \end{align*}$ We need $x^2+3xy + c(y) = 2y + 3xy+ y^2 + k(x)$ to make this happen, we set $c(y) = 2y+y^2$ and $k(x) = x^2$ . From this we find our potential function is $F(x,y) = x^2+3xy+ y^2 + 2y$ .

Now try your hand at these questions:

Is $\vec {G} = \vector {2x+y^2,2y+x^2}$ a gradient field? If so find a potential function.

yes no

Is $\vec {G} = \vector {x^3,-y^4}$ a gradient field? If so find a potential function.

yes no

Find a potential function $F$ such that $F(\vec {0}) = 0$ . $F(x,y) = \answer {x^4/4-y^5/5}.$

Is $\vec {G} = \vector {y\cos (x),\sin (x)}$ a gradient field? If so find a potential function.

yes no

Find a potential function $F$ such that $F(\vec {0}) = 0$ . $F(x,y) = \answer {y\sin (x)}.$

Is $\vec {G} = \vector {\frac {-y}{x^2+y^2},\frac {x}{x^2+y^2}}$ a gradient field? If so find a potential function.

yes no

What happens at $\vec {0}$ ?