|
(b)On the interval , is : more than
one of the above |
|
(c)On the interval , is : more than
one of the above |
(d)On the interval , is : more than
one of the above |
Please answer each of these questions to the best of your ability. You are welcome to re-watch parts of any of the videos to help you.
The graph of the function f is shown below.
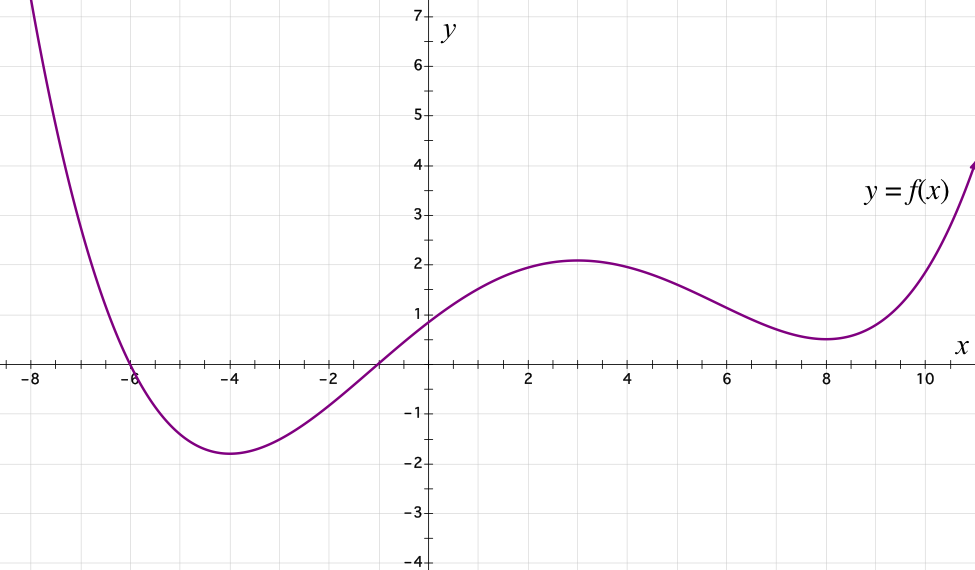
For this problem, use the graph above.
For this problem, use the graph above.
|
(b)On the interval , is : increasing decreasing more than one of the above |
|
(c)On the interval , is : increasing decreasing more than one of the above |
(d)On the interval , is : increasing decreasing more than one of the above |