Pre-Video Questions

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

To go back to the list of video sets, click HERE.

Before watching the videos, think about and answer these questions to the best of your ability.

The graph of the function $g$ is shown below.

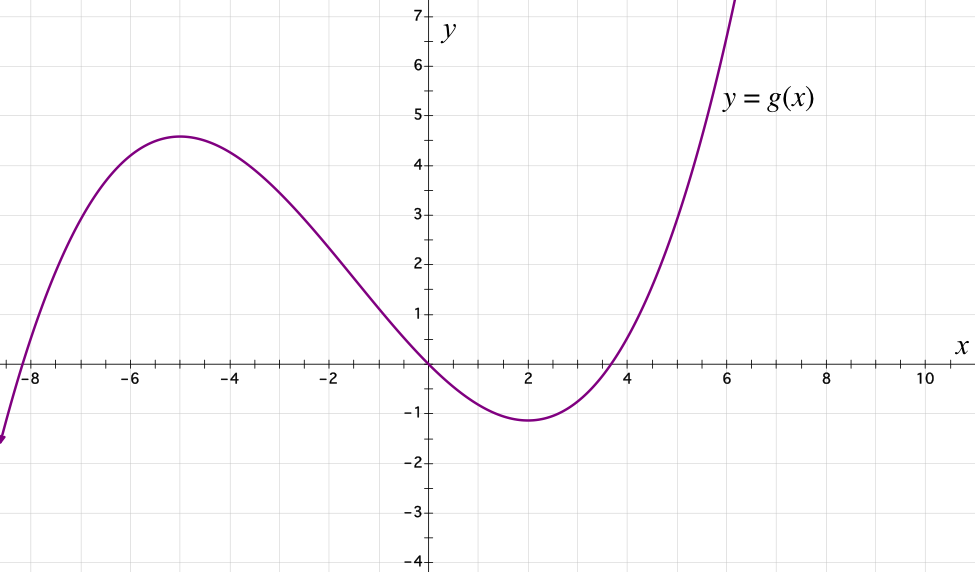
For this problem, use the graph above.

(a) On the interval $[-6, -4]$ , is $g'(x)$ : $<0$ $=0$ $>0$ more than one of the above	(b)On the interval $[-4, -2]$ , is $g'(x)$ : $<0$ $=0$ $>0$ more than one of the above
(c)On the interval $[0, 2]$ , is $g'(x)$ : $<0$ $=0$ $>0$ more than one of the above	(d)On the interval $[2, 4]$ , is $g'(x)$ : $<0$ $=0$ $>0$ more than one of the above

For this problem, use the graph above.

(a) On the interval $[-6, -4]$ , is $g'(x)$ : increasing decreasing more than one of the above	(b)On the interval $[-4, -2]$ , is $g'(x)$ : increasing decreasing more than one of the above
(c)On the interval $[0, 2]$ , is $g'(x)$ : increasing decreasing more than one of the above	(d)On the interval $[2, 4]$ , is $g'(x)$ : increasing decreasing more than one of the above

For how many values of $x$ in the interval $[-8, 6]$ does $g'(x)=0$ ? $\answer [format=integer]{2}$

From following expressions, identify the smallest and largest according to the numerical value they represent:

Largest:

$g'(8)$ $\dfrac {g(8+\Delta x)-g(8)}{\Delta x}$ for $\Delta x > 0$ $g(0)$ $g'(0)$

Smallest:

$g'(8)$ $\dfrac {g(8+\Delta x)-g(8)}{\Delta x}$ for $\Delta x > 0$ $g(0)$ $g'(0)$

Overall, how confident are you in your answers?

Not at all confident Not very confident Somewhat confident Very Confident